
【題目】已知,在平面直角坐標系xOy中,函數y=![]() (x>0)的圖象與一次函數y=kx﹣k的圖象的交點為A(m,2).
(x>0)的圖象與一次函數y=kx﹣k的圖象的交點為A(m,2).
(1)求一次函數的解析式;
(2)設一次函數y=kx﹣k的圖象與y軸交于點B,若P是x軸上一點,且滿足△PAB的面積是6,求點P的坐標.

【答案】(1)y=2x﹣2;(2)P點坐標為(4,0),(﹣2,0).
【解析】
(1)將A點坐標代入y=![]() (x>0),求出m的值為2,再將(2,2)代入y=kx﹣k,求出k的值,即可得到一次函數的解析式;
(x>0),求出m的值為2,再將(2,2)代入y=kx﹣k,求出k的值,即可得到一次函數的解析式;
(2)將三角形以x軸為分界線,分為兩個三角形計算,再把它們相加.
解:(1)根據題意,將點A(m,2)代入y=![]() ,
,
得:2=![]() ,
,
解得:m=2,
即點A(2,2),
將點A(2,2)代入y=kx﹣k,得:2=2k﹣k,
解得:k=2,
∴一次函數的解析式為y=2x﹣2;
(2)如圖,
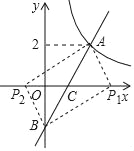
∵一次函數y=2x﹣2與x軸的交點為C(1,0),與y軸的交點為B(0,﹣2),
S△ABP=S△ACP+S△BPC,
∴![]() ×2CP+
×2CP+![]() ×2CP=6,
×2CP=6,
解得CP=3,
則P點坐標為(4,0),(﹣2,0).


科目:初中數學 來源: 題型:
【題目】新定義:若∠α的度數是∠β的度數的n倍,則∠α叫做∠β的n倍角.
(1)若∠M=10°21′,請直接寫出∠M的3倍角的度數;
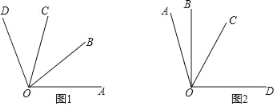
(2)如圖1,若∠AOB=∠BOC=∠COD,請直接寫出圖中∠AOB的所有2倍角;
(3)如圖2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“低碳環保”已經成為一種生活理念,同時也帶來無限商機.某高科技發展公司投資2000萬元成功研制出一種市場需求量較大的低碳高科技產品.已知生產每件產品的成本是40元,在銷售過程中發現:當銷售單價定為100元時,年銷售量為20萬件;銷售單價每增加10元,年銷售量將減少1萬件,設銷售單價為x(元),年銷售量為y(萬件),年獲利為z(萬元).(年獲利=年銷售額﹣生產成本﹣投資)
(1)試寫出z與x之間的函數關系式;
(2)請通過計算說明,到第一年年底,當z取最大值時,銷售單價x定為多少?此時公司是盈利了還是虧損了?
(3)若該公司計劃到第二年年底獲利不低于1130萬元,請借助函數的大致圖象說明,第二年的銷售單價x(元)應確定在什么范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y= ![]() 與雙曲線y=
與雙曲線y= ![]() (k>0,x>0)交于點A,將直線y=
(k>0,x>0)交于點A,將直線y= ![]() 向上平移4個單位長度后,與y軸交于點C,與雙曲線y=
向上平移4個單位長度后,與y軸交于點C,與雙曲線y= ![]() (k>0,x>0)交于點B,若OA=3BC,則k的值為( )
(k>0,x>0)交于點B,若OA=3BC,則k的值為( )
A.3
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
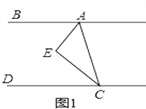
(1)請判斷AB與CD的位置關系并說明理由;
(2)如圖2,在(1)的結論下,當∠E=90°保持不變,移動直角頂點E,使∠MCE=∠ECD,當直角頂點E點移動時,問∠BAE與∠MCD是否存在確定的數量關系?

(3)如圖3,在(1)的結論下,P為線段AC上一定點,點Q為直線CD上一動點,當點Q在射線CD上運動時(點C除外)∠CPQ+∠CQP與∠BAC有何數量關系? (2、3小題只需選一題說明理由)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(中考·安徽)如圖,已知反比例函數y=![]() 與一次函數y=k2x+b的圖象交于A(1,8),B(-4,m).
與一次函數y=k2x+b的圖象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面積;
(3)若M(x1,y1),N(x2,y2)是反比例函數y=![]() 的圖象上的兩點,且x1<x2,y1<y2,指出點M,N位于哪個象限,并簡要說明理由.
的圖象上的兩點,且x1<x2,y1<y2,指出點M,N位于哪個象限,并簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅游商品經銷店欲購進A、B兩種紀念品,若用380元購進A種紀念品7件,B種紀念品8件;也可以用380元購進A種紀念品10件,B種紀念品6件.
(1)求A、B兩種紀念品的進價分別為多少?
(2)若該商店每銷售1件A種紀念品可獲利5元,每銷售1件B種紀念品可獲利7元,該商店準備用不超過900元購進A、B兩種紀念品40件,且這兩種紀念品全部售出時總獲利不低于216元,問應該怎樣進貨,才能使總獲利最大,最大為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com