
【題目】如圖,在Rt△ABC中∠BAC=90°,D,E分別是AB,BC的中點,F在CA的延長線上∠FDA=∠B,AC=6,AB=8,則四邊形AEDF的周長為_____.

 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線l為y=![]() x,過點A1(1,0)作A1B1⊥x軸,與直線l交于點B1,以原點O為圓心,OB1長為半徑畫圓弧交x軸于點A2;再作A2B2⊥x軸,交直線l于點B2,以原點O為圓心,OB2長為半徑畫圓弧交x軸于點A3;……,按此作法進行下去,則點An的坐標為(_______).
x,過點A1(1,0)作A1B1⊥x軸,與直線l交于點B1,以原點O為圓心,OB1長為半徑畫圓弧交x軸于點A2;再作A2B2⊥x軸,交直線l于點B2,以原點O為圓心,OB2長為半徑畫圓弧交x軸于點A3;……,按此作法進行下去,則點An的坐標為(_______).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果二次函數![]() 的圖象與
的圖象與![]() 軸有兩個公共點,那么一元二次方程
軸有兩個公共點,那么一元二次方程![]() 有兩個不相等的實根,請根據你對這句話的理解,解決下列問題:若
有兩個不相等的實根,請根據你對這句話的理解,解決下列問題:若![]() 、
、![]() (
(![]() <
<![]() )是關于的方程
)是關于的方程![]() 的兩根,且
的兩根,且![]() <
<![]() 則
則![]() 、
、![]() 、
、![]() 、
、![]() 的大小關系是( )
的大小關系是( )
A. ![]() <
<![]() <
<![]() <
<![]() B.
B. ![]() <
<![]() <
<![]() <
<![]()
C. ![]() <
<![]() <
<![]() <
<![]() D.
D. ![]() <
<![]() <
<![]() <
<![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,![]() ,點
,點![]() 為
為![]() 內一點,
內一點,![]() ,
,![]() 分別是點
分別是點![]() 關于
關于![]() 、
、![]() 的對稱點,連接
的對稱點,連接![]() ,分別交
,分別交![]() 于
于![]() 、
、![]() 于
于![]() .如果
.如果![]() ,
,![]() 的周長為
的周長為![]() ,
,![]() 的度數為
的度數為![]() ,請根據以上信息完成作圖,并指出
,請根據以上信息完成作圖,并指出![]() 和
和![]() 的值( )
的值( )

A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著地鐵和共享單車的發展,“地鐵![]() 單車”已成為很多市民出行的選擇
單車”已成為很多市民出行的選擇![]() 張老師從學校站出發,先乘坐地鐵到某一站出地鐵,再騎共享單車回家,設他出地鐵的站點與學校距離為
張老師從學校站出發,先乘坐地鐵到某一站出地鐵,再騎共享單車回家,設他出地鐵的站點與學校距離為![]() 單位:千米
單位:千米![]() ,乘坐地鐵的時間為
,乘坐地鐵的時間為![]() 單位分鐘
單位分鐘![]() ,經測量,得到如下數據:
,經測量,得到如下數據:
地鐵站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根據表中數據的規律,直接寫出表格中a、b的值和
根據表中數據的規律,直接寫出表格中a、b的值和![]() 關于x的函數表達式;
關于x的函數表達式;
![]() 張老師騎單車的時間
張老師騎單車的時間![]() 單位:分鐘
單位:分鐘![]() 也受x的影響,其關系可以用
也受x的影響,其關系可以用![]() 米描述,
米描述,
![]() 若張老師出地鐵的站點與學校距離為14千米,請求出張老師從學校回到家所需的時間;
若張老師出地鐵的站點與學校距離為14千米,請求出張老師從學校回到家所需的時間;
![]() 若張老師準備在離家較近的A,B,C,D,E中的某一站出地鐵,請問:張老師應選擇在哪一站出地鐵,才能使他從學校回到家所需的時間最短?并求出最短時間.
若張老師準備在離家較近的A,B,C,D,E中的某一站出地鐵,請問:張老師應選擇在哪一站出地鐵,才能使他從學校回到家所需的時間最短?并求出最短時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
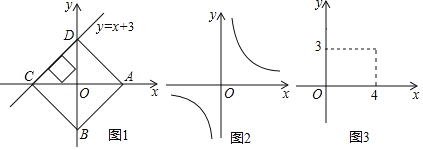
【題目】已知點A、B分別是x軸、y軸上的動點,點C、D是某個函數圖象上的點,當四邊形![]() 、B、C、D各點依次排列
、B、C、D各點依次排列![]() 為正方形時,我們稱這個正方形為此函數圖象的“伴侶正方形”,例如:在圖1中,正方形ABCD是一次函數
為正方形時,我們稱這個正方形為此函數圖象的“伴侶正方形”,例如:在圖1中,正方形ABCD是一次函數![]() 圖象的其中一個“伴侶正方形”.
圖象的其中一個“伴侶正方形”.
![]() 如圖1,若某函數是一次函數
如圖1,若某函數是一次函數![]() ,求它的圖象的所有“伴侶正方形”的邊長;
,求它的圖象的所有“伴侶正方形”的邊長;
![]() 如圖2,若某函數是反比例函數
如圖2,若某函數是反比例函數![]() ,它的圖象的“伴侶正方形”為ABCD,點
,它的圖象的“伴侶正方形”為ABCD,點![]() 在反比例函數圖象上,求m的值及反比例函數的解析式;
在反比例函數圖象上,求m的值及反比例函數的解析式;
![]() 如圖3,若某函數是二次函數
如圖3,若某函數是二次函數![]() ,它的圖象的“伴侶正方形”為ABCD,點C坐標為
,它的圖象的“伴侶正方形”為ABCD,點C坐標為![]() ,請你直接寫出該二次函數的解析式.
,請你直接寫出該二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
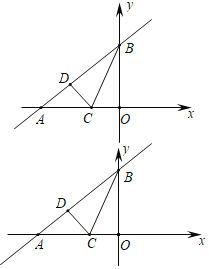
【題目】已知:直線y=![]() x+3與x軸、y軸分別相于點A和點B,點C在線段AO上.
x+3與x軸、y軸分別相于點A和點B,點C在線段AO上.
將△CBO沿BC折疊后,點O恰好落在AB邊上點D處
(1)求直線BC的解析式;
(2)求點D的坐標;
(3)P為平面內一動點,且以A、B、C、P為頂點的四邊形為平行四邊形,直接寫出點P坐標 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題情境:如圖,在Rt△ABC中,∠ACB=90°∠BAC=30°.
動手操作:(1)若以直角邊AC所在的直線為對稱軸.將Rt△ABC作軸對稱變換,請你在原圖上作出它的對稱圖形:
觀察發現:(2)Rt△ABC和它的對稱圖形組成了什么圖形?你最準確的判斷是 .
合作交流:(3)根據上面的圖形,請你猜想直角邊BC與斜邊AB的數量關系,并證明你的猜想.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是等邊三角形ABC外接圓⊙O上的點,在以下判斷中,不正確的是

A、當弦PB最長時,ΔAPC是等腰三角形 B、當ΔAPC是等腰三角形時,PO⊥AC
C、當PO⊥AC時,∠ACP=300 D、當∠ACP=300時,ΔPBC是直角三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com