
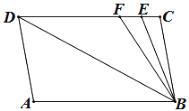
【題目】如圖,已知直線(xiàn)AB∥CD,∠A=∠C=100°,E、F在CD上,且滿(mǎn)足∠DBF=∠ABD,BE平分∠CBF.
(1)直線(xiàn)AD與BC有何位置關(guān)系?請(qǐng)說(shuō)明理由.
(2)求∠DBE的度數(shù).
(3)若把AD左右平行移動(dòng),在平行移動(dòng)AD的過(guò)程中,是否存在某種情況,使∠BEC=∠ADB?若存在,求出此時(shí)∠ADB的度數(shù);若不存在,請(qǐng)說(shuō)明理由.
【答案】(1) AD∥BC,理由見(jiàn)解析;(2) 40°;(3)存在,∠ADB=60°
【解析】試題分析:(1)根據(jù)平行線(xiàn)的性質(zhì),以及等量代換證明∠ADC+∠C=180°,即可證得AD∥BC;(2)由直線(xiàn)AB∥CD,根據(jù)兩直線(xiàn)平行,同旁?xún)?nèi)角互補(bǔ),即可求得∠ABC的度數(shù),又由∠DBE=![]() ∠ABC,即可求得∠DBE的度數(shù).
∠ABC,即可求得∠DBE的度數(shù).
(3)首先設(shè)∠ABD=∠DBF=∠BDC=x°,由直線(xiàn)AB∥CD,根據(jù)兩直線(xiàn)平行,同旁?xún)?nèi)角互補(bǔ)與兩直線(xiàn)平行,內(nèi)錯(cuò)角相等,可求得∠BEC與∠ADB的度數(shù),又由∠BEC=∠ADB,即可得方程:x°+40°=80°-x°,解此方程即可求得答案.
試題解析:(1)AD∥BC
理由:∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°-∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=![]() ∠ABF+
∠ABF+![]() ∠CBF=
∠CBF=![]() ∠ABC=40°;
∠ABC=40°;
(3)存在.
理由:設(shè)∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°-∠A=80°,
∴∠ADB=80°-x°.
若∠BEC=∠ADB,
則x°+40°=80°-x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.


 能考試全能100分系列答案
能考試全能100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
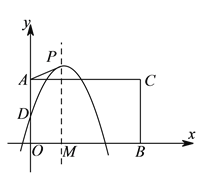
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)![]() ,
, ![]() 分別是
分別是![]() 軸正半軸,
軸正半軸, ![]() 軸正半軸上兩動(dòng)點(diǎn),
軸正半軸上兩動(dòng)點(diǎn), ![]() ,
, ![]() ,以
,以![]() ,
, ![]() 為鄰邊構(gòu)造矩形
為鄰邊構(gòu)造矩形![]() ,拋物線(xiàn)
,拋物線(xiàn)![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
, ![]() 為頂點(diǎn),
為頂點(diǎn), ![]() 軸于點(diǎn)
軸于點(diǎn)![]() .
.
(![]() )求
)求![]() ,
, ![]() 的長(zhǎng)(結(jié)果均用含
的長(zhǎng)(結(jié)果均用含![]() 的代數(shù)式表示);
的代數(shù)式表示);
(![]() )當(dāng)
)當(dāng)![]() 時(shí),求該拋物線(xiàn)的表達(dá)式;
時(shí),求該拋物線(xiàn)的表達(dá)式;
(![]() )在點(diǎn)
)在點(diǎn)![]() 在整個(gè)運(yùn)動(dòng)過(guò)程中,若存在
在整個(gè)運(yùn)動(dòng)過(guò)程中,若存在![]() 是等腰三角形,請(qǐng)求出所有滿(mǎn)足條件的
是等腰三角形,請(qǐng)求出所有滿(mǎn)足條件的![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】把二次函數(shù)y=a(x-h)2+k的圖象先向左平移2個(gè)單位,再向上平移4個(gè)單位,得到二次函數(shù)y=![]() (x+1)2-1的圖象.
(x+1)2-1的圖象.
(1)試確定a,h,k的值;
(2)指出二次函數(shù)y=a(x-h)2+k的開(kāi)口方向,對(duì)稱(chēng)軸和頂點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2020年2月初,在抵御新冠肺炎的工作中,全國(guó)各地口罩嚴(yán)重供應(yīng)不足,某鄉(xiāng)鎮(zhèn)企業(yè)縫紉車(chē)間立即轉(zhuǎn)崗做口罩以供應(yīng)本地志愿者和衛(wèi)生系統(tǒng),該車(chē)間有技術(shù)工人15人,生產(chǎn)部為了合理制定口罩的日生產(chǎn)定額,統(tǒng)計(jì)了15人某天加工口罩?jǐn)?shù)如下:
車(chē)間15名工人某一天加工口罩個(gè)數(shù)統(tǒng)計(jì)表
加工零件數(shù)/個(gè) | 540 | 450 | 300 | 240 | 210 | 120 |
人數(shù) | 1 | 1 | 2 | 6 | 3 | 2 |
(1)求這一天15名工人加工口罩?jǐn)?shù)的平均數(shù)、中位數(shù)和眾數(shù).
(2)為了提高大多數(shù)工人的積極性,管理者準(zhǔn)備試行“每天定額生產(chǎn),超產(chǎn)有獎(jiǎng)”的措施,假如你是管理者,從平均數(shù)、中位數(shù)、眾數(shù)的角度進(jìn)行分析,你將如何確定這個(gè)“定額”?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
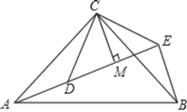
【題目】如圖,△ACB和△DCE均為等腰三角形,∠ACB=∠DCE=90°,點(diǎn)A、D、E在同一直線(xiàn)上,CM為△DCE中DE邊上的高,連接BE.
(1)求∠AEB的度數(shù);
(2)線(xiàn)段CM、AE、BE之間存在怎樣的數(shù)量關(guān)系?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1) 如圖1,正方形ABCD的邊長(zhǎng)為5,點(diǎn)E是AB上一點(diǎn),點(diǎn)F是AD延長(zhǎng)線(xiàn)上一點(diǎn),且BE=DF,四邊形AEGF是矩形,寫(xiě)出矩形AEGF的面積y與BE的長(zhǎng)x之間的函數(shù)關(guān)系式;
(2) 如圖2,已知一長(zhǎng)方形打印紙長(zhǎng)20 cm,寬15 cm,現(xiàn)在要在打印紙上打印文稿,上下左右各留出一定距離.設(shè)留出的距離均為x cm,打印文稿面積為y cm2,試寫(xiě)出y與x之間的關(guān)系式,并求出x的取值范圍.
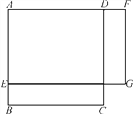
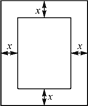
圖1 圖2
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某小區(qū)改善生態(tài)環(huán)境,實(shí)行生活垃圾的分類(lèi)處理,將生活垃圾分成三類(lèi):廚房垃圾、可回收垃圾和其他垃圾,分別記為m,n,p,并且設(shè)置了相應(yīng)的垃圾箱,“廚房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分別記為A,B,C.
(1)若將三類(lèi)垃圾隨機(jī)投入三類(lèi)垃圾箱,請(qǐng)用畫(huà)樹(shù)狀圖的方法求垃圾投放正確的概率;
(2)為了了解居民生活垃圾分類(lèi)投放的情況,現(xiàn)隨機(jī)抽取了小區(qū)三類(lèi)垃圾箱中總共1 000噸生活垃圾,數(shù)據(jù)統(tǒng)計(jì)如下(單位:噸):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
請(qǐng)根據(jù)以上信息,試估計(jì)“廚房垃圾”投放正確的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平行四邊形ABCD,尺規(guī)作圖:以點(diǎn)A為圓心,AB的長(zhǎng)為半徑畫(huà)弧交AD于點(diǎn)F,分別以點(diǎn)B,F為圓心,以大于 BF的長(zhǎng)為半徑畫(huà)弧交于點(diǎn)G,做射線(xiàn)AG交BC與點(diǎn)E,若BF=12,AB=10,則AE的長(zhǎng)為( ).

A.17B.16C.15D.14
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在△ABC中,AB=AC,D、E是BC邊上的點(diǎn),連接AD、AE,以△ADE的邊AE所在直線(xiàn)為對(duì)稱(chēng)軸作△ADE的軸對(duì)稱(chēng)圖形△AD′E,連接D′C,若BD=CD′.
(1)求證:△ABD≌△ACD′;
(2)如圖2,若∠BAC=120°,探索BD,DE,CE之間滿(mǎn)足怎樣的數(shù)量關(guān)系時(shí),△CD′E是正三角形;
(3)如圖3,若∠BAC=90°,求證:DE2=BD2+EC2.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com