【題目】如圖，直線y=x+2與拋物線y=ax2+bx+6（a≠0）相交于A（
，
）和B（4，m），點P是線段AB上異于A、B的動點，過點P作PC⊥x軸于點D，交拋物線于點C．當△PAC為直角三角形時點P的坐標 ．
【答案】（3，5）或（
，
）．
【解析】
試題分析：由于P點不可能為直角頂點，因此就只有兩種情況：若A為直角頂點，過A作AB的垂線與拋物線的交點即為C點，過C作y軸的平行線與AB的交點即為P點；若C為直角頂點，過A作x軸的平行線與拋物線的另一個交點即為C點，過C作y軸的平行線與AB的交點即為P點．
解：∵直線y=x+2過點B（4，m），
∴m=6，
∴B（4，6）．
將A、B兩點坐標代入拋物線解析式得：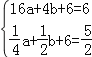
，
解得：
∴拋物線的解析式為：y=2x2﹣8x+6．
①若A為直角頂點，如圖1，
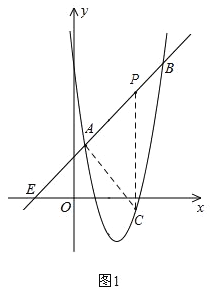
設AC的解析式為：y=﹣x+b，
將A點代入y=﹣x+b得b=3
∴AC的解析式為y=﹣x+3，
由
，解得：
或
（舍去）
令P點的橫坐標為3，則縱坐標為5，
∴P（3，5）；
②若C為直角頂點，如圖2，
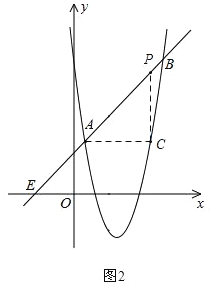
令
，解得：x=或x=
（舍去），
令P點的橫坐標為，則縱坐標為，
∴P（，）；
故答案為：（3，5）或（，）．
走進文言文系列答案科目：初中數學 來源： 題型：
【題目】閱讀下面解答過程，填空或填理由．
已知如圖，點E，F分別是AB和CD上的點，DE，AF分別交BC于點G，H，∠A＝∠D，∠1＝∠2.試說明：∠B＝∠C.
解：∵∠1＝∠2 ( )，
∠2＝∠3 ( )，
∴∠3＝∠1 ( )．
∴AF∥DE ( )．
∴∠4＝∠D ( )．
又∵∠A＝∠D ( ），
∴∠A＝∠4 ( )．
∴AB∥CD ( )．
∴∠B＝∠C ( )．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法中，正確的是（ ）
A. 有一個角為直角的四邊形是菱形
B. 對角線互相垂直的菱形是正方形
C. 對角線相等的平行四邊形是矩形
D. 一組鄰邊相等的平行四邊形是正方形
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將數字“6”旋轉180°，得到數字“9”；將數字“9”旋轉180°，得到數字“6”．現將數字“69”旋轉180°，得到的數字是（ ）
A. 96 B. 69 C. 66 D. 99
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
