
【題目】如圖,直線AB、CD被直線AC所截,AB∥CD,E是平面內任意一點(點E不在直線AB、CD、AC上),設∠BAE=α,∠DCE=β.下列各式:①α+β;②α-β;③β-α;④180°-α-β中.∠AEC的度數可能是 _____(把正確答案的序號填在橫線上).

科目:初中數學 來源: 題型:
【題目】按照有關規定,距高鐵軌道![]() 米以內的區域內不宜臨路新建學校、醫院、敬老院和集中住宅區等噪聲敏感建筑物.如圖是一個小區平面示意圖,長方形
米以內的區域內不宜臨路新建學校、醫院、敬老院和集中住宅區等噪聲敏感建筑物.如圖是一個小區平面示意圖,長方形![]() 為一新建小區,直線
為一新建小區,直線![]() 為高鐵軌道,
為高鐵軌道,![]() 是直線
是直線![]() 上的兩點,點
上的兩點,點![]() 在一條直線上,且
在一條直線上,且![]() .小王看中了
.小王看中了![]() 號樓
號樓![]() 單元的一套住宅,與售樓人員的對話如下:
單元的一套住宅,與售樓人員的對話如下:
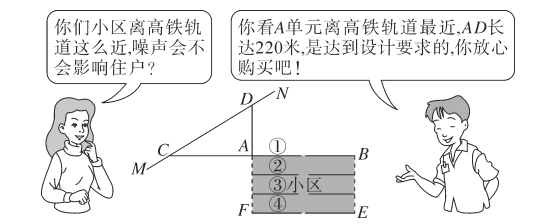
![]() 小王心中一算,發現售樓人員的話不可信,請你用所學的數學知識說明理由;
小王心中一算,發現售樓人員的話不可信,請你用所學的數學知識說明理由;
![]() 若一列長度為
若一列長度為![]() 米的高鐵以
米的高鐵以![]() 千米/時的速度通過,則
千米/時的速度通過,則![]() 單元用戶受到影響的時間有多長?
單元用戶受到影響的時間有多長?
(參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從1、2、3、4中任取一個數作為十位上的數字,再從余下的數字中任取一個數作為個位上的數字,那么組成的兩位數是6的倍數的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD折疊,使點D與點B重合,點C落在C′處,折痕為EF,若AB=1,BC=2,則△ABE和△BC′F的周長之和為( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知MB=ND,∠MBA=∠NDC,下列哪個條件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AM∥CN,點B為平面內一點,AB⊥BC于B.

(1)如圖1,直接寫出∠A和∠C之間的數量關系___;
(2)如圖2,過點B作BD⊥AM于點D,求證:∠ABD=∠C;
(3)如圖3,在(2)問的條件下,點E. F在DM上,連接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y= ![]() (x+2)(x﹣4)與x軸交于點A,B(點A位于點B的左側),與y軸交于點C,CD∥x軸交拋物線于點D,M為拋物線的頂點.
(x+2)(x﹣4)與x軸交于點A,B(點A位于點B的左側),與y軸交于點C,CD∥x軸交拋物線于點D,M為拋物線的頂點.
(1)求點A,B,C的坐標;
(2)設動點N(﹣2,n),求使MN+BN的值最小時n的值;
(3)P是拋物線上一點,請你探究:是否存在點P,使以P,A,B為頂點的三角形與△ABD相似(△PAB與△ABD不重合)?若存在,求出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點![]() 的坐標為
的坐標為![]() ,
,![]() 與
與![]() 軸交于點
軸交于點![]() ,且
,且![]() 為
為![]() 的中點,雙曲線
的中點,雙曲線![]() 經過
經過![]() 、
、![]() 兩點.
兩點.

(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如圖1,點![]() 在
在![]() 軸上,若四邊形
軸上,若四邊形![]() 是平行四邊形,求點
是平行四邊形,求點![]() 的坐標;
的坐標;
(3)如圖2,在(2)的條件下,動點![]() 在雙曲線
在雙曲線![]() 上,點
上,點![]() 在
在![]() 軸上,若以
軸上,若以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形,試求滿足要求的所有點
為頂點的四邊形為平行四邊形,試求滿足要求的所有點![]() 、
、![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校為了解學生對新聞、體育、動畫、娛樂、戲曲類電視節目的喜愛情況,采用抽樣的方法在七年級選取了一個班的同學,通過問卷調查,收集數據、整理數據,制作了如下兩個整統計圖,請根據下面兩個不完整的統計圖分析數據,回答以下問題:

(1)七年級的這個班共有學生_____人,圖中![]() ______,
______,![]() ______,在扇形統計圖中,“體育”類電視節目對應的圓心角為:______.
______,在扇形統計圖中,“體育”類電視節目對應的圓心角為:______.
(2)補全條形統計圖;
(3)根據抽樣調查的結果,估算該校1750名學生中大約有多少人喜歡“娛樂”類電視節目?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com