
【題目】AD是△ABC的高,AC=2 ![]() ,AD=4,把△ADC沿著直線AD對折,點C落在點E的位置,如果△ABE是等腰三角形,那么線段BE的長度為( )
,AD=4,把△ADC沿著直線AD對折,點C落在點E的位置,如果△ABE是等腰三角形,那么線段BE的長度為( )
A.2 ![]()
B.2 ![]() 或5
或5
C.2 ![]()
D.5
【答案】B
【解析】解:如圖 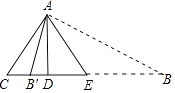
①當高AD在△ABC內時,由題意EA=EB=AC=2 ![]() .
.
②當高AD在△ACB′外時,設AB′=B′E=x.
在Rt△ADC中,CD= ![]() =
= ![]() =2,
=2,
由題意DE=DC=2,
在Rt△AED中,∵AB′2=AD2+DB′2 ,
∴x2=42+(x﹣2)2 ,
∴x=5.
∴線段BE的長度為2 ![]() 或5,
或5,
故選B.
【考點精析】本題主要考查了等腰三角形的性質和翻折變換(折疊問題)的相關知識點,需要掌握等腰三角形的兩個底角相等(簡稱:等邊對等角);折疊是一種對稱變換,它屬于軸對稱,對稱軸是對應點的連線的垂直平分線,折疊前后圖形的形狀和大小不變,位置變化,對應邊和角相等才能正確解答此題.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩名射手在相同條件下打靶,射中的環數如圖所示,利用圖中提供的信息,解答下列問題:
(1)分別求甲、乙兩名射手中環數的眾數和平均數;
(2)如果從甲、乙兩名射手中選一名去參加射擊比賽,你選誰去?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,則BD的長是( )
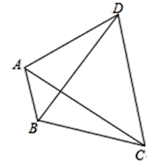
A. 5 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,一次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() .
.
(1)若點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() 在一次函數
在一次函數![]() 的圖象上,求
的圖象上,求![]() 的值;
的值;
(2)求由直線![]() ,(1)中的直線
,(1)中的直線![]() 以及
以及![]() 軸圍成的三角形的面積.
軸圍成的三角形的面積.
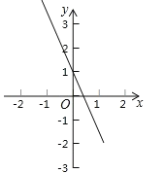
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB和CD相交于O點,OE⊥CD,OC平分∠AOF,∠EOF=56°,
(1)求∠BOD的度數;
(2)寫出圖中所有與∠BOE互余的角,它們分別是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BF平分∠ABC,AF⊥BF于點F,D為AB的中點,連接DF延長交AC于點E.若AB=10,BC=18,則線段EF的長為( ) 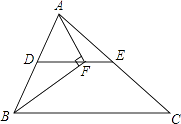
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(10,0),(0,4),點D是OA的中點,點P在BC上運動,當△ODP是腰長為5的等腰三角形時,點P的坐標為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com