
【題目】在數軸上,點A向右移動1個單位得到點B,點B向右移動(n+1)(n為正整數)個單位得到點C,點A、B、C分別表示有理數a、b、c.
(1)當n=1時,A、B、C三點在數軸上的位置如圖所示,a、b、c三個數的乘積為正數.
![]()
①數軸上原點的位置可能( )
A.在點A左側或在A、B兩點之間
B.在點C右側或在A、B兩點之間
C.在點A左側或在B、C兩點之間
D.在點C右側或在B、C兩點之間
②若這三個數的和與其中的一個數相等,則a=_________(簡述理由)
(2)將點C向右移動(n+2)個單位得到點D,點D表示有理數d,a、b、c、d四個數的積為正數,且這四個數的和與其中的兩個數的和相等,a為整數,若n分別取1,2,3,…,100時,對應的a的值分別記為![]() ,…,
,…,![]() ,則
,則![]() .
.
【答案】(1)①C;②-2或![]() ,理由見解析;(2)-2650.
,理由見解析;(2)-2650.
【解析】
(1)①把n=1代入即可得出AB=1,BC=2,再根據a、b、c三個數的乘積為正數即可選擇出答案;
②b=a+1,c=a+3.分三種情況討論:當a+a+1+a+3=a時;當a+a+1+a+3=a+1時;當a+a+1+a+3=a+3時.分別解方程即可;
(2)依據題意得:b=a+1,c=b+n+1=a+n+2,d=c+n+2=a+2n+4.根據a、b、c、d四個數的積為正數,且這四個數的和與其中的兩個數的和相等,即可得出用含n的式子表示a,由a為整數,分兩種情況討論:當n為奇數時;當n為偶數時,得出a1,a2,a3,a4,…,a99,a100,從而得出結論.
(1)①把n=1代入即可得出AB=1,BC=2.
∵a、b、c三個數的乘積為正數,∴從而可得出在點A左側或在B、C兩點之間.
故選C;
②b=a+1,c=a+3.分三種情況討論:
當a+a+1+a+3=a時,a=﹣2;
當a+a+1+a+3=a+1時,a![]() ;
;
當a+a+1+a+3=a+3時,a![]() (舍去).
(舍去).
綜上所述:a=-2或![]() .
.
(2)依據題意得:b=a+1,c=b+n+1=a+n+2,d=c+n+2=a+2n+4.
∵a、b、c、d四個數的積為正數,且這四個數的和與其中的兩個數的和相等,∴a+c=0或b+c=0.∴a![]() 或a
或a![]() ;
;
∵a為整數,∴當n為奇數時,a![]() ,當n為偶數時,a
,當n為偶數時,a![]() ,∴a1=﹣2,a2=﹣2,a3=﹣3,a4=﹣3,…,a99=﹣51,a100=﹣51,∴a1+a2+a3+…+a100=-2(2+3+...+50+51)=-2×
,∴a1=﹣2,a2=﹣2,a3=﹣3,a4=﹣3,…,a99=﹣51,a100=﹣51,∴a1+a2+a3+…+a100=-2(2+3+...+50+51)=-2×![]() =﹣2650.
=﹣2650.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC內部的一個動點,且滿足∠PAB=∠PBC,則線段CP長的最小值為( ) 
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,則下列結論不正確的是
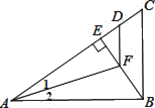
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過A(﹣2,0)B(﹣3,3)及原點O,頂點為C.
(1)求拋物線的解析式;
(2)若點E在拋物線的對稱軸上,且A、O、D、E為頂點是四邊形是平行四邊形,求點D的坐標.
(3)P是拋物線上的第一象限內的動點,過點P作PM⊥x軸,垂足為M,是否存在點P,使得以P、M、A為頂點的三角形△BOC相似?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上三點M,O,N對應的數分別為-1,0,3,點P為數軸上任意一點,其對應的數為x.
![]()
(1)MN的長為 ;
(2)如果點P到點M、點N的距離相等,那么x的值是 ;
(3)數軸上是否存在點P,使點P到點M、點N的距離之和是8?若存在,直接寫出x的值;若不存在,請說明理由.
(4)如果點P以每分鐘1個單位長度的速度從點O向左運動,同時點M和點N分別以每分鐘2個單位長度和每分鐘3個單位長度的速度也向左運動.設t分鐘時點P到點M、點N的距離相等,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,都是由邊長為 1 的正方體疊成的立體圖形,例如第⑴個圖形由 1 個正方體疊成,第⑵個圖形由 4 個正方體疊成,第⑶個圖形由 10 個正方體疊成,依次規律,第⑺個圖形由( )個正方形疊成.

A. 86 B. 87 C. 85 D. 84
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,BF平分∠ABC,交AD于點F,CE平分∠BCD,交AD于點E,AB=3,EF=1,則BC長為( ) 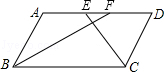
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,E為BC邊上的一點,連結AE、BD且AE=AB. 
(1)求證:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】黃石市在創建國家級文明衛生城市中,綠化檔次不斷提升.某校計劃購進A,B兩種樹木共100棵進行校園綠化升級,經市場調查:購買A種樹木2棵,B種樹木5棵,共需600元;購買A種樹木3棵,B種樹木1棵,共需380元.
(1)求A種,B種樹木每棵各多少元?
(2)因布局需要,購買A種樹木的數量不少于B種樹木數量的3倍.學校與中標公司簽訂的合同中規定:在市場價格不變的情況下(不考慮其他因素),實際付款總金額按市場價九折優惠,請設計一種購買樹木的方案,使實際所花費用最省,并求出最省的費用.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com