
【題目】如圖,在△ABC中,∠ACB=90°,點E,F在邊AB上,將邊AC沿CE翻折,使點A落在AB上的點D處,再將邊BC沿CF翻折,使點B落在CD的延長線上的點B'處.

(1)求∠ECF的度數;
(2)若CE=4,B'F=1,求線段BC的長和△ABC的面積.
【答案】(1)∠ECF=45°;(2)BC=![]() ,和△ABC的面積為
,和△ABC的面積為![]() .
.
【解析】
(1)由折疊可得,∠ACE=∠DCE=![]() ∠ACD,∠BCF=∠B'CF=
∠ACD,∠BCF=∠B'CF=![]() ∠BCB',再根據∠ACB=90°,即可得出∠ECF=45°;
∠BCB',再根據∠ACB=90°,即可得出∠ECF=45°;
(2)在Rt△BCE中,根據勾股定理可得BC=![]() ,設AE=x,則AB=x+5,根據勾股定理可得AE2+CE2=AB2﹣BC2,即x2+42=(x+5)2﹣41,求得x=
,設AE=x,則AB=x+5,根據勾股定理可得AE2+CE2=AB2﹣BC2,即x2+42=(x+5)2﹣41,求得x=![]() ,即可得出S△ABC=
,即可得出S△ABC=![]() AB×CE=
AB×CE=![]() .
.
解:(1)由折疊可得,∠ACE=∠DCE=![]() ∠ACD,∠BCF=∠B'CF=
∠ACD,∠BCF=∠B'CF=![]() ∠BCB',
∠BCB',
又∵∠ACB=90°,
∴∠ACD+∠BCB'=90°,
∴∠ECD+∠FCD=![]() ×90°=45°,
×90°=45°,
即∠ECF=45°;
(2)由折疊可得,∠DEC=∠AEC=90°,BF=B'F=1,
∴∠EFC=45°=∠ECF,
∴CE=EF=4,
∴BE=4+1=5,
∴再Rt△BCE中,BC=![]()
設AE=x,則AB=x+5,
∵在Rt△ACE中,AC2=AE2+CE2,
在Rt△ABC中,AC2=AB2﹣BC2,
∴AE2+CE2=AB2﹣BC2,
即x2+42=(x+5)2﹣41,
解得x=![]()
∴S△ABC=![]() AB×CE=
AB×CE=![]() (
(![]() +5)×4=
+5)×4=![]() .
.


科目:初中數學 來源: 題型:
【題目】甲、乙兩個批發店銷售同一種蘋果,在甲批發店,不論一次購買數量是多少,價格均為6元/kg.在乙批發店,一次購買數量不超過50kg時,價格均為7元/kg;一次性購買超過50kg時,其中有50kg的價格仍為7元/kg,超過50kg的部分價格為5元/kg.設小王在同一個批發店一次購買蘋果的數量為![]() kg(
kg(![]() >0)
>0)
(1)根據題意填表:a= b=
一次購買數量(kg) | 30 | 50 | 150 | … |
甲批發店花費(元) | 180 | 300 | 900 | … |
乙批發店花費(元) | a | 350 | b | … |
(2)設在甲批發店花費![]() 元,在乙批發店花費
元,在乙批發店花費![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)若小王在同一個批發店一次性購買蘋果花費了360元,則他在甲、乙兩個批發店中批發,哪個批發店購買數量多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,與CD相交于點F,H是BC邊的中點,連結DH與BE相交于點G.
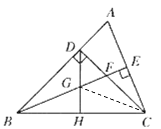
(1)求證:BF=AC;
(2)求證:CE=![]() BF;
BF;
(3)CE與BG的大小關系如何?試證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種優質蜜柚,投入市場銷售時,經調查,該蜜柚每天銷售量y(千克)與銷售單價x(元/千克)之間符合一次函數關系,如圖所示.

(1)求y與x的函數關系式;
(2)某農戶今年共采摘該蜜柚4500千克,其保質期為40天,若以18元/千克銷售,問能否在保質期內銷售完這批蜜柚?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正面分別寫著數字1,2,3的三張卡片(注:這三張卡片的形狀、大小、質地,顏色等其他方面完全相同,若背面上放在桌面上,這三張卡片看上去無任何差別)洗勻后,背面向上放在桌面上,從中先隨機抽取一張卡片,記該卡片上的數字為x,再把剩下的兩張卡片洗勻后,背面向上放在桌面上,再從這兩張卡片中隨機抽取一張卡片,記該卡片上的數字為y.
(1)用列表法或樹狀圖法(樹狀圖也稱樹形圖)中的一種方法,寫出(x,y)所有可能出現的結果.
(2)求取出的兩張卡片上的數字之和為偶數的概率P.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市今年中考理化實驗操作考試,采用學生抽簽方式決定自己的考試內容.規定:每位考生必須在三個物理實驗(用紙簽A、B、C表示)和三個化學實驗(用紙簽D、E、F表示)中各抽取一個進行考試,小剛在看不到紙簽的情況下,分別從中各隨機抽取一個.
(1) 用“列表法”或“樹狀圖法”表示所有可能出現的結果;
(2) 小剛抽到物理實驗B和化學實驗F(記作事件P)的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學生對待學習的態度一直是教育工作者關注的問題之一.為此,某區教委對該區部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:

(1)此次抽樣調查中,共調查了 名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
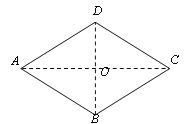
【題目】已知:如圖,四邊形ABCD是菱形,AB=AD.
求證:(1) AB=BC=CD=DA
(2) AC⊥DB
(3) ∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com