
 如圖在直角坐標(biāo)系中,將矩形OABC沿OB對折,使點A落在點A1處,OA=8,OC=4,則△BDO的面積為________,點A1的坐標(biāo)為________.
如圖在直角坐標(biāo)系中,將矩形OABC沿OB對折,使點A落在點A1處,OA=8,OC=4,則△BDO的面積為________,點A1的坐標(biāo)為________. ,
, )
)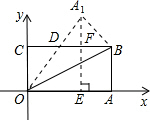 解:(1)∵BC∥AO,
解:(1)∵BC∥AO, ×5×4=10;
×5×4=10; OA•AB=
OA•AB= ×8×4=16,S△BDO=10.
×8×4=16,S△BDO=10. BD•A1F=
BD•A1F= ×5A1F=6,
×5A1F=6, ,
, ,
, x,
x, )代入得,
)代入得, =
= a,
a, ,
, ,
, ).
). ,
, ).
).

科目:初中數(shù)學(xué) 來源: 題型:
 24、(北師大版)如圖在直角坐標(biāo)系中,右邊的圖案是由左邊的圖案經(jīng)過平移以后得到的.左圖案中左右眼睛的坐標(biāo)分別是(-4,2)、(-2,2),右圖中左眼的坐標(biāo)是(3,4),則右圖案中右眼的坐標(biāo)是
24、(北師大版)如圖在直角坐標(biāo)系中,右邊的圖案是由左邊的圖案經(jīng)過平移以后得到的.左圖案中左右眼睛的坐標(biāo)分別是(-4,2)、(-2,2),右圖中左眼的坐標(biāo)是(3,4),則右圖案中右眼的坐標(biāo)是查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
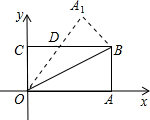 如圖在直角坐標(biāo)系中,將矩形OABC沿OB對折,使點A落在點A1處,OA=8,OC=4,則△BDO的面積為
如圖在直角坐標(biāo)系中,將矩形OABC沿OB對折,使點A落在點A1處,OA=8,OC=4,則△BDO的面積為查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:

| 4 | 3 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com