
【題目】△ABD中,AB=BD,點C在直線BD上,BD=3CD,cos∠CAD= ![]() ,AD=6,則AC= .
,AD=6,則AC= .
【答案】6或 ![]()
【解析】解:分兩種情況:①如圖所示,當點C在線段BD上時,過B作BF⊥AD于F,過D作DE⊥AD交AC的延長線于E,

Rt△ADE中,cos∠CAD= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AE= ![]() , 分兩種情況:①如圖所示,當點C在線段BD上時,過B作BF⊥AD于F,過D作DE⊥AD交AC的延長線于E,在Rt△ADE中根據銳角三角函數的定義得出AE的長,
, 分兩種情況:①如圖所示,當點C在線段BD上時,過B作BF⊥AD于F,過D作DE⊥AD交AC的延長線于E,在Rt△ADE中根據銳角三角函數的定義得出AE的長,
∵BD=3CD,DE∥BF,
∴ ![]() =
= ![]() =
= ![]() ,
,
設CE=x,則CG=2x,GE=3x,
∵AB=BD,BF⊥AD,
∴AF=FD,
∴AG=GE=3x,
∴AE=6x,AC=5x,
∴AC= ![]() AE=
AE= ![]() ×
× ![]() =6;②如圖所示,當C在BD的延長線上時,過B作BF⊥AD于F,過C作CE⊥AD交AD的延長線于E,
=6;②如圖所示,當C在BD的延長線上時,過B作BF⊥AD于F,過C作CE⊥AD交AD的延長線于E,
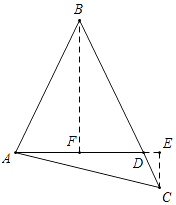
∵AB=BD,BF⊥AD,
∴AF=FD= ![]() AD=3,
AD=3,
∵CE∥BF,BD=3CD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即DE=1,
,即DE=1,
∴AE=6+1=7,
∵Rt△ACE中,cos∠CAD= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AC= ![]() .
.
綜上所述,AC的長為6或 ![]() .
.
所以答案是:6或 ![]() .
.
【考點精析】解答此題的關鍵在于理解等腰三角形的性質的相關知識,掌握等腰三角形的兩個底角相等(簡稱:等邊對等角),以及對平行線分線段成比例的理解,了解三條平行線截兩條直線,所得的對應線段成比例.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,∠ABC=90°,AB=BC,過△ABC的頂點B作直線![]() ,且點A到
,且點A到![]() 的距離為2,點C到
的距離為2,點C到![]() 的距離為3,則AC的長是( )
的距離為3,則AC的長是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=ax2+bx+2過點A(﹣2,0),B(2,2),與y軸交于點C.
(1)求拋物線y=ax2+bx+2的函數表達式;
(2)若點D在拋物線y=ax2+bx+2的對稱軸上,求△ACD的周長的最小值;
(3)在拋物線y=ax2+bx+2的對稱軸上是否存在點P,使△ACP是直角三角形?若存在直接寫出點P的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P為平行四邊形ABCD邊AD上一點,E、F分別為PB、PC的中點,△PEF、△PDC、△PAB的面積分別為S、S1、S2 , 若S=2,則S1+S2= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某體育用品商場為推銷某一品牌運動服,先做了市場調查,得到數據如下表:
賣出價格x(元/件) | 50 | 51 | 52 | 53 |
銷售量P(件) | 500 | 490 | 480 | 470 |
則P與x的函數關系式為________,當賣出價格為60元時,銷售量為_______件.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于實數p,q,我們用符號min{p,q}表示p,q兩數中較小的數,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,則x= .
}=;若min{(x﹣1)2 , x2}=1,則x= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】湖州素有魚米之鄉之稱,某水產養殖大戶為了更好地發揮技術優勢,一次性收購了 ![]()
![]() 淡水魚,計劃養殖一段時間后再出售.已知每天放養的費用相同,放養
淡水魚,計劃養殖一段時間后再出售.已知每天放養的費用相同,放養 ![]() 天的總成本為
天的總成本為 ![]() 萬元;放養
萬元;放養 ![]() 天的總成本為
天的總成本為 ![]() 萬元(總成本=放養總費用+收購成本).
萬元(總成本=放養總費用+收購成本).
(1)設每天的放養費用是 ![]() 萬元,收購成本為
萬元,收購成本為 ![]() 萬元,求
萬元,求 ![]() 和
和 ![]() 的值;
的值;
(2)設這批淡水魚放養 ![]() 天后的質量為
天后的質量為 ![]() (
( ![]() ),銷售單價為
),銷售單價為 ![]() 元/
元/ ![]() .根據以往經驗可知:
.根據以往經驗可知: ![]() 與
與 ![]() 的函數關系為
的函數關系為 ![]() ;
; ![]() 與
與 ![]() 的函數關系如圖所示.
的函數關系如圖所示.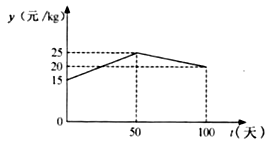
①分別求出當 ![]() 和
和 ![]() 時,
時, ![]() 與
與 ![]() 的函數關系式;
的函數關系式;
②設將這批淡水魚放養 ![]() 天后一次性出售所得利潤為
天后一次性出售所得利潤為 ![]() 元,求當
元,求當 ![]() 為何值時,
為何值時, ![]() 最大?并求出最大值.(利潤=銷售總額-總成本)
最大?并求出最大值.(利潤=銷售總額-總成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面文字,然后回答問題.
大家知道![]() 是無理數,而無理數是無限不循環小數,所以
是無理數,而無理數是無限不循環小數,所以![]() 的小數部分我們不可能全部寫出來,由于
的小數部分我們不可能全部寫出來,由于![]() 的整數部分是1,將
的整數部分是1,將![]() 減去它的整數部分,差就是它的小數部分,因此
減去它的整數部分,差就是它的小數部分,因此![]() 的小數部分可用
的小數部分可用![]() ﹣1表示.
﹣1表示.
由此我們得到一個真命題:如果![]() =x+y,其中x是整數,且0<y<1,那么x=1,y=
=x+y,其中x是整數,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
請解答下列問題:
(1)如果![]() =a+b,其中a是整數,且0<b<1,那么a= ,b= ;
=a+b,其中a是整數,且0<b<1,那么a= ,b= ;
(2)如果﹣![]() =c+d,其中c是整數,且0<d<1,那么c= ,d= ;
=c+d,其中c是整數,且0<d<1,那么c= ,d= ;
(3)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com