
【題目】如圖,已知![]() 半徑為
半徑為![]() ,弦
,弦![]() 垂直平分半徑
垂直平分半徑![]() ,并交
,并交![]() 于點
于點![]() .
.
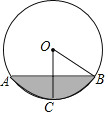
(1)求弦![]() 的長;
的長;
(2)求弧![]() 的長,并求出圖中陰影部分面積.
的長,并求出圖中陰影部分面積.
【答案】(1)10![]() cm;(2)
cm;(2)![]() cm,
cm,![]() cm2.
cm2.
【解析】
(1)先利用垂徑定理得出AB=2BD,∠ODB=90°,OD=![]() OC=5,進而根據勾股定理求出BD,即可得出結論;
OC=5,進而根據勾股定理求出BD,即可得出結論;
(2)先利用銳角三角函數求出∠BOD=60°,最后利用扇形的弧長公式和扇形的面積公式即可得出結論.
(1)如圖,⊙O半徑為10cm,
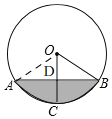
∴OB=OC=10,
∵弦AB垂直平分半徑OC,
∴AB=2BD,∠ODB=90°,OD=![]() OC=5,
OC=5,
在Rt△BOD中,根據勾股定理得,BD=![]() ,
,
∴AB=2BD=10![]() cm;
cm;
(2)由(1)知,OD=5,
在Rt△BOD中,cos∠BOD=![]() ,
,
∴∠BOD=60°,
∵OC⊥AB,
∴∠AOB=2∠BOD=120°,
∴弧![]() cm,
cm,
S陰影=S扇形AOB-S△AOB=![]() (cm2).
(cm2).


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】(問題)用n個2×1矩形,鑲嵌一個2×n矩形,有多少種不同的鑲嵌方案?(2×n矩形表示矩形的鄰邊是2和n)
(探究)不妨假設有an種不同的鑲嵌方案.為探究an的變化規律,我們采取一般問題特殊化的策略,先從最簡單情形入手,再逐次遞進,最后猜想得出結論.
探究一:用1個2×1矩形,鑲嵌一個2×1矩形,有多少種不同的鑲嵌方案?
如圖(1),顯然只有1種鑲嵌方案.所以,a1=1.
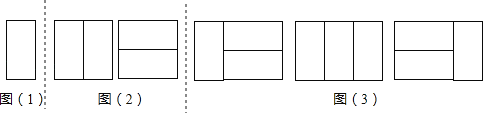
探究二:用2個2×1矩形,鑲嵌一個2×2矩形,有多少種不同的鑲嵌方案?
如圖(2),顯然只有2種鑲嵌方案.所以,a2=2.
探究三:用3個2×1矩形,鑲嵌一個2×3矩形,有多少種不同的鑲嵌方案?
一類:在探究一每個鑲嵌圖的右側再橫著鑲嵌2個2×1矩形,有1種鑲嵌方案;
二類:在探究二每個鑲嵌圖的右側再豎著鑲嵌1個2×1矩形,有2種鑲嵌方案;
如圖(3).所以,a3=1+2=3.
探究四:用4個2×1矩形,鑲嵌一個2×4矩形,有多少種不同的鑲嵌方案?
一類:在探究二每個鑲嵌圖的右側再橫著鑲嵌2個2×1矩形,有 種鑲嵌方案;
二類:在探究三每個鑲嵌圖的右側再豎著鑲嵌1個2×1矩形,有 種鑲嵌方案;
所以,a4= .
探究五:用5個2×1矩形,鑲嵌一個2×5矩形,有多少種不同的鑲嵌方案?
(仿照上述方法,寫出探究過程,不用畫圖)
……
(結論)用n個2×1矩形,鑲嵌一個2×n矩形,有多少種不同的鑲嵌方案?
(直接寫出an與an﹣1,an﹣2的關系式,不寫解答過程).
(應用)用10個2×1矩形,鑲嵌一個2×10矩形,有 種不同的鑲嵌方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD內接于⊙O,AB=AC,BD⊥AC,垂足為E,點F在BD的延長線上,且DF=DC,連接AF、CF.
(1)求證:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
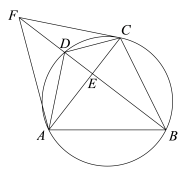
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 為常數)交
為常數)交![]() 軸于點
軸于點![]() ,與
,與![]() 軸的一個交點在
軸的一個交點在![]() 和
和![]() 之間,頂點為
之間,頂點為![]() .
.
①拋物線![]() 與直線
與直線![]() 有且只有一個交點;
有且只有一個交點;
②若點![]() 、點
、點![]() 、點
、點![]() 在該函數圖象上,則
在該函數圖象上,則![]()
③將該拋物線向左平移![]() 個單位,再向下平移
個單位,再向下平移![]() 個單位,所得拋物線解析式為
個單位,所得拋物線解析式為![]() ;
;
④點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() 點
點![]() 分別在
分別在![]() 軸和
軸和![]() 軸上,當
軸上,當![]() 時,四邊形
時,四邊形![]() 周長的最小值為
周長的最小值為![]() .
.
其中正確判斷的序號是( )
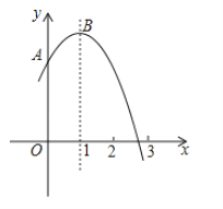
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() 中,
中,![]() 為
為![]() 內一點,將
內一點,將![]() 繞點
繞點![]() 按逆時針方向旋轉角
按逆時針方向旋轉角![]() 得到
得到![]() ,點
,點![]() 的對應點分別為點
的對應點分別為點![]() ,且
,且![]() 三點在同一直線上.
三點在同一直線上.
(1)填空:![]() (用含
(用含![]() 的代數式表示);
的代數式表示);
(2)如圖2,若![]() ,請補全圖形,再過點
,請補全圖形,再過點![]() 作
作![]() 于點
于點![]() ,然后探究線段
,然后探究線段![]() 之間的數量關系,并證明你的結論;
之間的數量關系,并證明你的結論;
(3)若![]() ,且點
,且點![]() 滿足
滿足![]() ,直接寫出點
,直接寫出點![]() 到
到![]() 的距離.
的距離.
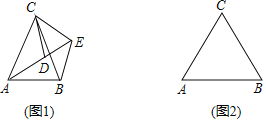
查看答案和解析>>
科目:初中數學 來源: 題型:
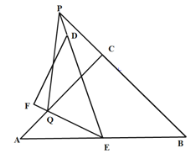
【題目】如圖,△ABC和△DEF都是等腰直角三角形,∠ACB=∠EFD=90,△DEF,的頂點E與△ABC的斜邊AB的中點重合.將△DEF繞點E旋轉,旋轉過程中,線段AC與線段EF相交于點Q,射線ED與射線BC相交于點P.
(1)求證:△AEQ∽△BPE;
(2)求證:PE平分∠BPQ;
(3)當AQ=2,AE=![]() ,求PQ的長.
,求PQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,2分別是某款籃球架的實物圖與示意圖,已知底座BC=0.60米,底座BC與支架AC所成的角∠ACB=75°,支架AF的長為2.50米,籃板頂端F點到籃框D的距離FD=1.35米,籃板底部支架HE與支架AF所成的角∠FHE=60°,求籃框D到地面的距離(精確到0.01米)(參考數據:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一枚均勻的正四面體,四個面上分別標有數字1,2,3,4,小紅隨機地拋擲一次,把著地一面的數字記為x;另有三張背面完全相同,正面上分別寫有數字-2,-1,1的卡片,小亮將其混合后,正面朝下放置在桌面上,并從中隨機地抽取一張,把卡片正面上的數字記為y;然后他們計算出S=x+y的值.
(1)用樹狀圖或列表法表示出S的所有可能情況;
(2)分別求出當S=0和S<2時的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com