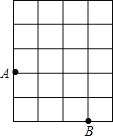
【題目】如圖，A、B是網格中的兩個格點，點C也是網格中的一個格點，連接AB、BC、AC，當△ABC為等腰三角形時，格點C的不同位置有 處，設網格中的每個小正方形的邊長為1，則所有滿足題意的等腰三角形ABC的面積之和等于 ．
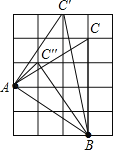
【答案】3；15．
【解析】
試題分析：根據AB的長度確定C點的不同位置，由已知條件，利用勾股定理可知AB=
，然后即可確定C點的位置；
計算這三個三角形的面積時，△ABC的面積直接用
×4×3得出，其它兩個三角形面積可用正方形面積減去多余三角形的面積即可，例如三角形ABC′的面積用正方形面積20減去2個相等的三角形面積，再減去梯形的面積即可．
解：格點C的不同位置分別是：C、C′、C″，
∵網格中的每個小正方形的邊長為1，
∴S△ABC=
×4×3=6，
S△ABC′=20﹣2×3﹣
=6.5，
S△ABC″=2.5，
∴S△ABC+S△ABC′+S△ABC″=6+6.5+2.5=15．
故答案分別為：3；15．
智能訓練練測考系列答案
計算高手系列答案科目：初中數學 來源： 題型：
【題目】已知n邊形的內角和θ=（n-2）×180°.
（1）甲同學說，θ能取360°；而乙同學說，θ也能取630°.甲、乙的說法對嗎？若對，求出邊數n.若不對，說明理由；
（2）若n邊形變為（n+x）邊形，發現內角和增加了360°，用列方程的方法確定x.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠1=∠3，CD∥EF，試說明∠1=∠4．請將過程填寫完整．
解：∵∠1=∠3，
又∠2=∠3(_______)，
∴∠1=____，
∴______∥______(_______)，
又∵CD∥EF，
∴AB∥_____，
∴∠1=∠4(兩直線平行，同位角相等).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面文字，然后回答問題．
大家知道
是無理數，而無理數是無限不循環小數，所以的小數部分我們不可能全部寫出來，由于的整數部分是1，將 減去它的整數部分，差就是它的小數部分，因此的小數部分可用﹣1表示．
由此我們得到一個真命題：如果＝x+y，其中x是整數，且0＜y＜1，那么x＝1，y＝﹣1．
請解答下列問題：
（1）如果
＝a+b，其中a是整數，且0＜b＜1，那么a＝ ，b＝ ；
（2）如果﹣＝c+d，其中c是整數，且0＜d＜1，那么c＝ ，d＝ ；
（3）已知2+＝m+n，其中m是整數，且0＜n＜1，求|m﹣n|的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在紙面上有一數軸（如圖），折疊紙面．
（1）若表示1的點與表示
的點重合，則表示
的點與表示 的點重合；
（2）若表示的點與表示3的點重合，回答以下問題：
①表示5的點與表示 的點重合：
②若數軸上
、
兩點之間的距離為14（在的左側），且、兩點經折疊后重合，求、兩點表示的數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】設a、b、c是△ABC的三條邊,關于x的方程x2+2
x+2c-a=0有兩個相等的實數根，方程3cx+2b=2a的根為0.
（1）求證：△ABC為等邊三角形；
（2）若a,b為方程x2+mx-3m=0的兩根，求m的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠B+∠BCD=180°，∠B=∠D.
求證：∠E=∠DFE.
證明：∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD （ ）
∴∠B=_______（ ）
又∵∠B=∠D（已知 ）,
∴∠D=_______( )
∴AD∥BE（ ）
∴∠E=∠DFE（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知整數a0，a1，a2，a3，a4，…，滿足下列條件：a0＝0，a1＝﹣|a0+1|，a2＝﹣|a1+2|，a3＝﹣|a2+3|，…，以此類推，a2019的值是（ ）
A. ﹣1009B. ﹣1010C. ﹣2018D. ﹣2020
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
