Question

【題目】某批乒乓球的質量檢驗結果如下：

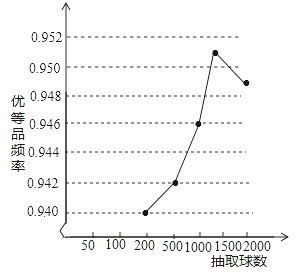
（1）畫出這批乒乓球“優等品”頻率的折線統計圖；

（2）這批乒乓球“優等品”的概率的估計值是多少？

（3）從這批乒乓球中選擇5個黃球、13個黑球、22個紅球，它們除顏色外都相同，將它們放入一個不透明的袋中．

①求從袋中摸出一個球是黃球的概率；

②現從袋中取出若干個黑球，并放入相同數量的黃球，攪拌均勻后使從袋中摸出一個是黃球的概率不小于，問至少取出了多少個黑球？

Answer 1

【答案】（1）答案見解析；（2）0.946；（3）①；②9．

【解析】試題分析：（1）根據統計表中的數據，先描出各點，然后折線連結即可；

（2）根據頻率估計概率，頻率都在0.946左右波動，所以可以估計這批乒乓球“優等品”概率的估計值是0.946；

（3）①用黃球的個數除以球的總個數即可；

②設從袋中取出了x個黑球，根據攪拌均勻后使從袋中摸出一個是黃球的概率不小于，列出不等式，解不等式即可．

試題解析：解：（1）如圖；

（2）這批乒乓球“優等品”概率的估計值是0.946；

（3）①∵袋中一共有球5+13+22=40個，其中有5個黃球，∴從袋中摸出一個球是黃球的概率為： =；

②設從袋中取出了x個黑球，由題意得： ，解得x≥，故至少取出了9個黑球．