【題目】拋物線y=ax2+bx+c的頂點為D（–1，2），與x軸的一個交點A在點（–3，0）和（–2，0）之間，其部分圖象如下圖，則以下結論：①b2–4ac<0；②a+b+c<0；③c–a=2；④方程ax2+bx+c–2=0有兩個相等的實數根．其中正確結論的個數為（ ）
A. 1個 B. 2個 C. 3個 D. 4個
【答案】C
【解析】試題分析：由拋物線與x軸有兩個交點，可知b2-4ac＞0，所以①錯誤；
由拋物線的頂點為D（-1，2），可知拋物線的對稱軸為直線x=-1，然后由拋物線與x軸的一個交點A在點（-3，0）和（-2，0）之間，可知拋物線與x軸的另一個交點在點（0，0）和（1，0）之間，因此當x=1時，y＜0，即a+b+c＜0，所以②正確；
由拋物線的頂點為D（-1，2），可知a-b+c=2，然后由拋物線的對稱軸為直線x=
=-1，可得b=2a，因此a-2a+c=2，即c-a=2，所以③正確；
由于當x=-1時，二次函數有最大值為2，即只有x=-1時，ax2+bx+c=2，因此方程ax2+bx+c-2=0有兩個相等的實數根，所以④正確．
故選：C．
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，點E在AB上，把△ABC沿CE折疊后，點B恰好與斜邊AC的中點D重合.
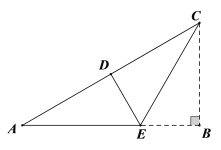
(1)求證：△ACE為等腰三角形；
(2)若AB=6，求AE的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】要建一個如圖所示的面積為300
的長方形圍欄，圍欄總長50m，一邊靠墻（墻長25m），
（1）求圍欄的長和寬；
（2）能否圍成面積為400 的長方形圍欄？如果能，求出該長方形的長和寬，如果不能請說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義
表示不大于x的最大整數，例如
，
，
．
（1）將
、
、按照從小到大的順序用不等號連接：_______________；
（2）利用（1）中的結論，方程
的解為___________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示是二次函數
圖象的一部分，圖象過點
，二次函數圖象對稱軸為直線
，給出五個結論：①
；②
；③當
時，
隨
的增大而增大；④方程
的根為
，
；⑤
其中正確結論是（ ）
A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某超市銷售某種玩具，進貨價為
元．根據市場調查：在一段時間內，銷售單價是
元時，銷售量是
件，而銷售單價每上漲
元，就會少售出
件玩具，超市要完成不少于
件的銷售任務，又要獲得最大利潤，則銷售單價應定為________元．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（問題探究）
將三角形
紙片沿
折疊，使點A落在點
處.
（1）如圖，當點A落在四邊形
的邊
上時，直接寫出
與
之間的數量關系；
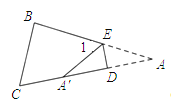
（2）如圖，當點A落在四邊形的內部時，求證：
；
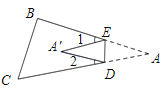
（3）如圖，當點A落在四邊形的外部時，探索，
，之間的數量關系，并加以證明；
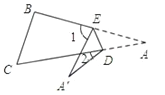
（拓展延伸）
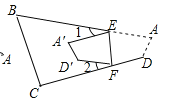
（4）如圖，若把四邊形
紙片沿
折疊，使點A、D落在四邊形
的內部點、
的位置，請你探索此時，，，
之間的數量關系，寫出你發現的結論，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
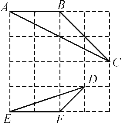
【題目】如圖，在4×4的正方形網格中，△ABC和△DEF的頂點都在邊長為1的正方形的頂點上．
(1)填空：∠ABC＝__________度，BC＝_________；
(2)求證：∠C＝∠E.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，Rt△ABC的三個頂點分別是A（－3，2），B（0，4），C（0，2）．
（1）將△ABC以點C為旋轉中心旋轉180°，畫出旋轉后對應的△
C；平移△ABC，若A的對應點
的坐標為（0，4），畫出平移后對應的△
；
（2）若將△C繞某一點旋轉可以得到△，請直接寫出旋轉中心的坐標；
（3）在
軸上有一點P，使得PA+PB的值最小，請直接寫出點P的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com