
【題目】數學課上,同學們遇到這樣一個問題:
如圖1,已知![]() ,
,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 與
與 ![]() 的角平分線,請同學們根據題中的條件提出問題,大家一起來解決(本題出現的角均小于平角)
的角平分線,請同學們根據題中的條件提出問題,大家一起來解決(本題出現的角均小于平角)
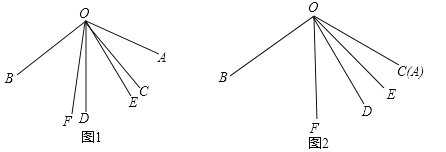
同學們經過思考后,交流了自己的想法:
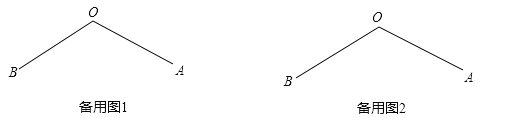
小強說:“如圖2,若![]() 與
與![]() 重合,且
重合,且![]() ,
,![]() 時,可求
時,可求![]() 的度數.”
的度數.”
小偉說:“在小強提出問題的前提條件下,將![]() 的
的![]() 邊從
邊從![]() 邊開始繞點
邊開始繞點![]() 逆時針
逆時針
轉動![]() ,可求出
,可求出![]() 的值.”
的值.”
老師說:“在原題的條件下,借助射線![]() 的不同位置可得出的數量關系.”
的不同位置可得出的數量關系.”
(1)請解決小強提出的問題;
(2)在備用圖1中,補充完整的圖形,并解決小偉提出的問題
(3)在備用圖2中,補充完整的圖形,并解決老師提出的問題,即求![]() 三者之間的的數量關系.
三者之間的的數量關系.
【答案】(1)45![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() 、
、![]()
![]() 、180
、180![]()
![]()
![]() 、180
、180![]()
![]()
![]() .
.
【解析】
(1)根據角平分線定義即可解決小強提出的問題;
(2)在備用圖1中,補充完整的圖形,根據角平分線定義及角的和差計算即可解決小偉提出的問題;
(3)在備用圖2中,補充完整的圖形,分四種情況討論即可解決老師提出的問題,進而求出![]() 三者之間的數量關系.
三者之間的數量關系.
(1)如圖2,
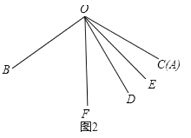
∵∠AOB=120![]() ,OF是∠BOC的角平分線
,OF是∠BOC的角平分線
∴∠FOC=![]() ∠AOB=60
∠AOB=60![]()
∵∠COD=30![]() ,OE是∠AOD的角平分線
,OE是∠AOD的角平分線
∴∠EOC=![]() ∠COD=15
∠COD=15![]()
∴∠EOF=∠FOC∠EOC=45![]()
答:∠EOF的度數為45![]() ;
;
(2)如圖3,
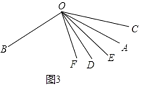
∵OE、OF分別是∠AOD與∠BOC的角平分線,
∴設∠AO=∠DOE=![]() ∠AOD=
∠AOD=![]()
∠BOF=∠COF=![]() ∠BOC=
∠BOC=![]()
∴∠BOE=∠AOB∠AOE=120![]()
![]()
∵∠BOC=∠AOB+∠COD∠AOD=150![]() 2
2![]()
∴∠COF=75![]()
![]()
∴∠DOF=∠COF∠COD=75![]()
![]() 30
30![]() =45°
=45°![]()
∴∠BOE∠DOF=(120![]()
![]() )((45
)((45![]()
![]() )=75
)=75![]()
∵∠COE=∠COD∠DOE=30![]()
![]()
∴∠EOF=∠FOC∠COE=(75![]() )(30
)(30![]()
![]() )=45
)=45![]()
∴![]() =
=![]()
答:![]() 的值為
的值為![]() ;
;
(3)∵OE、OF分別是∠AOD與∠BOC的角平分線,
∴設∠AOE=∠DOE=![]() ∠AOD=
∠AOD=![]()
∠BOF=∠COF=![]() ∠BOC
∠BOC
∴①如圖4,
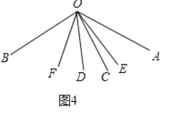
∠AOC=∠AOD∠COD=2![]() β
β
∵∠BOC=∠AOB∠AOC
=![]() (2
(2![]()
![]() )
)
=![]() 2
2![]() +
+![]()
∴∠FOC=![]() ∠BOC=
∠BOC=![]()
![]()
![]() +
+![]()
![]()
∵∠COE=∠DOE∠COD=![]()
![]()
∴∠EOF=∠FOC+∠COE
=![]()
![]()
![]() +
+![]()
![]() +
+![]()
![]()
=![]() (
(![]()
![]() ).
).
②如圖5,
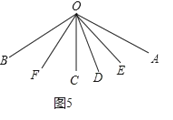
∠AOC=∠AOD+∠COD=2![]() +
+![]()
∵∠BOC=∠AOB∠AOC
=![]() (2
(2![]() +
+![]() )
)
=![]() 2
2![]()
![]()
∴∠FOC=![]() ∠BOC=
∠BOC=![]()
![]()
![]()
![]()
![]()
∵∠COE=∠DOE+∠COD=![]() +
+![]()
∴∠EOF=∠FOC+∠COE
=![]()
![]()
![]()
![]()
![]() +
+![]() +
+![]()
=![]() (
(![]() +
+![]() ).
).
③如圖6,
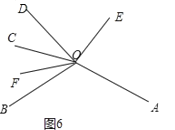
∠AOC=∠AOD+∠COD=2![]() +
+![]()
∵∠BOC=360![]() ∠AOB∠AOC
∠AOB∠AOC
=360![]()
![]() (2
(2![]() +
+![]() )
)
=360![]()
![]() 2
2![]()
![]()
∴∠FOC=![]() ∠BOC=180
∠BOC=180![]()
![]()
![]()
![]()
![]()
![]()
∵∠COE=∠DOE+∠COD=![]() +
+![]()
∴∠EOF=∠FOC+∠COE
=180![]()
![]()
![]()
![]()
![]()
![]() +
+![]() +
+![]()
=180![]()
![]() (
(![]()
![]() ).
).
④如圖7,
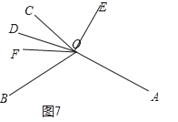
∠AOC=∠AOD∠COD=2![]()
![]()
∵∠BOC=360![]() ∠AOB∠AOC
∠AOB∠AOC
=360![]()
![]() (2
(2![]()
![]() )
)
=360![]()
![]() 2
2![]() +
+![]()
∴∠FOC=![]() ∠BOC=180
∠BOC=180![]()
![]()
![]()
![]() +
+![]()
![]()
∵∠COE=∠DOE∠COD=![]() β
β
∴∠EOF=∠FOC+∠COE
=180![]()
![]()
![]()
![]() +
+![]()
![]() +
+![]()
![]()
=180![]()
![]() (
(![]() +
+![]() ).
).
答:![]() 、β、∠EOF三者之間的數量關系為:
、β、∠EOF三者之間的數量關系為:![]() (
(![]()
![]() )、
)、![]() (
(![]() +
+![]() )、180
)、180![]()
![]() (
(![]()
![]() )、180
)、180![]()
![]() (
(![]() +
+![]() ).
).


科目:初中數學 來源: 題型:
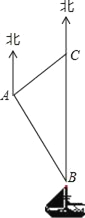
【題目】釣魚島是我國固有領土,現在我邊海漁民要在釣魚島附近進行捕魚作業,當漁船航行至B處時,測得該島位于正北方向20(1+![]() )海里的C處,為了防止某國海警干擾,請求我A處的魚監船前往C處護航,已知C位于A處的北偏東45°方向,A位于B的北偏西30°方向,求A、C之間的距離.
)海里的C處,為了防止某國海警干擾,請求我A處的魚監船前往C處護航,已知C位于A處的北偏東45°方向,A位于B的北偏西30°方向,求A、C之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,圖①是沿
的中點,圖①是沿![]() 將
將![]() 折疊,點
折疊,點![]() 落在
落在![]() 上,圖②是繞點
上,圖②是繞點![]() 將
將![]() 順時針旋轉
順時針旋轉![]() .
.
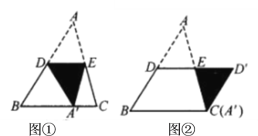
(1)在圖①中,判斷![]() 和
和![]() 形狀.(填空)_______________________________________
形狀.(填空)_______________________________________
(2)在圖②中,判斷四邊形![]() 的形狀,并說明理由.
的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為測量一座山峰CF的高度,將此山的某側山坡劃分為AB和BC兩段,每一段山坡近似是“直”的,測得坡長AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.則山峰的高度CF約為( )米.(可用的參考數據:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.則山峰的高度CF約為( )米.(可用的參考數據:sin50°≈0.8,tan50°≈1.2, ![]() )
)
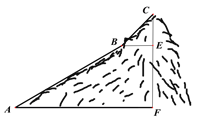
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中數學 來源: 題型:
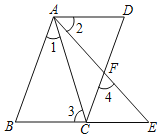
【題目】如圖,已知四邊形ABCD,AB∥CD,點E是BC延長線上一點,連接AC、AE,AE交CD于點F,∠1=∠2,∠3=∠4.
證明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩家超市以相同的價格出售同樣的商品,為了吸引顧客,各自推出不同的優惠方案:在甲超市累計購買商品超出300元之后,超出部分按原價8折優惠;在乙超市累計購買商品超出200元之后超過部分按原價85折優惠設顧客預計累計購物![]() 元(
元(![]() )
)
(1)請用含![]() 的代數式分別表示顧客在兩家超市購物所付的費用;
的代數式分別表示顧客在兩家超市購物所付的費用;
(2)某顧客分別到兩家超市買了相同的貨物,并且所付費用也相同你知道這位顧客共花了多少錢嗎?請列出方程解答.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數的圖象經過![]() ,
,![]() 兩點.
兩點.
(1)求這個一次函數的解析式;
(2)試判斷點![]() 是否在這個一次函數的圖象上;
是否在這個一次函數的圖象上;
(3)求此函數圖象與![]() 軸,
軸,![]() 軸圍成的三角形的面積.
軸圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知平面內兩點![]() .
.

(1)請用尺規按下列要求作圖,并保留作圖痕跡;
①連接![]() ;
;
②在線段![]() 的延長線上取點
的延長線上取點![]() ,使
,使![]() ;
;
③在線段![]() 的延長線上取點
的延長線上取點![]() ,使
,使![]() .
.
(2)請求出線段![]() 與線段
與線段![]() 長度之間的數量關系.
長度之間的數量關系.
(3)如果![]() ,則
,則![]() 的長度為________,
的長度為________,![]() 的長度為________,
的長度為________,![]() 的長度為_________.
的長度為_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com