Question

【題目】已知A是拋物線y2=4x上的一點，以點A和點B（2，0）為直徑的圓C交直線x=1于M，N兩點．直線l與AB平行，且直線l交拋物線于P，Q兩點．
（Ⅰ）求線段MN的長；
（Ⅱ）若 =﹣3，且直線PQ與圓C相交所得弦長與|MN|相等，求直線l的方程．

Answer 1

【答案】解：（Ⅰ）設A（ ，y0），則C的方程為（x﹣2）（x﹣ +y（y﹣y0）=0， 令x=1，得y2﹣y0y+ ﹣1=0，
∴|MN|=|y1﹣y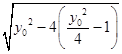2|= =2；
（Ⅱ）設直線l的方程為x=my+n，代入拋物線方程得y2﹣4my﹣4n=0，
∴y1+y2=4m，y1y2=﹣4n
∵ =﹣3，
∴x1x2+y1y2= +y1y2=﹣3，
∴n2﹣4n+3=0，
∴n=1或3，此時B（2，0）到直線l的距離d= ．
由題意，圓心C到直線l的距離等于到直線x=1的距離，
∴ = ．
∵m= ，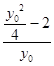
∴ =64，
∴ =8，
∴m=0，
∴直線l的方程為x=3，
綜上，直線l的方程為x=1或x=3．
【解析】（Ⅰ）C的方程為（x﹣2）（x﹣ +y（y﹣y0）=0，令x=1，得y2﹣y0y+ ﹣1=0，利用韋達定理及弦長公式求線段MN的長；（Ⅱ）設直線l的方程為x=my+n，代入拋物線方程，利用 =﹣3，求出n，直線PQ與圓C相交所得弦長與|MN|相等，求出m，即可求直線l的方程．