
【題目】為了了解市民“獲取新聞的最主要途徑”,某市記者開展了一次抽樣調查,根據調查結果繪制了如下尚不完整的統計圖:
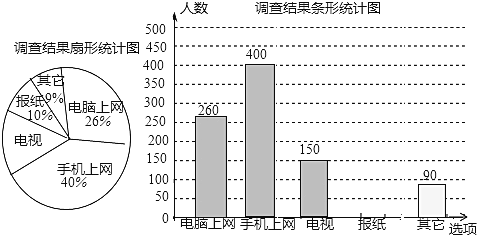
根據以上信息解答下列問題:
(1)這次接受調查的市民總人數是______;
(2)扇形統計圖中,“電視”所對應的圓心角的度數是______;
(3)請補全條形統計圖.
 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
【題目】已知一次函數![]() 的圖像經過點M(-1,3)、N(1,5)。直線MN與坐標軸相交于點A、B兩點.
的圖像經過點M(-1,3)、N(1,5)。直線MN與坐標軸相交于點A、B兩點.
(1)求一次函數的解析式.
(2)如圖,點C與點B關于x軸對稱,點D在線段OA上,連結BD,把線段BD順時針方向旋轉90°得到線段DE,作直線CE交x軸于點F,求![]() 的值.
的值.
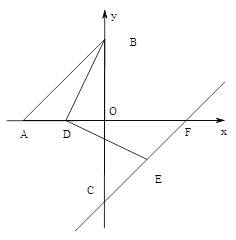
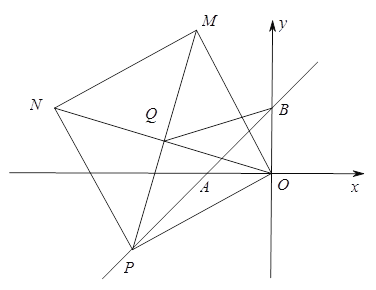
(3)如圖,點P是直線AB上一動點,以OP為邊作正方形OPNM,連接ON、PM交于點Q,連BQ,當點P在直線AB上運動時,![]() 的值是否會發生變化,若不變,請求出其值;若變化,請說明理由.
的值是否會發生變化,若不變,請求出其值;若變化,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E在AD的延長線上,下列條件中能判斷AB∥CD的是( )
A.∠C=∠CDEB.∠ABD=∠CBDC.∠ABD=∠CDBD.∠C+∠ADC=180°
查看答案和解析>>
科目:初中數學 來源: 題型:
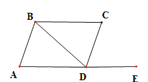
【題目】如圖,將口ABCD的邊DC延長到點E,使CE=DC,連接AE,交BC于點F.
(1)求證:△ABF≌△ECF
(2)若∠AFC=2∠D,連接AC、BE.求證:四邊形ABEC是矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
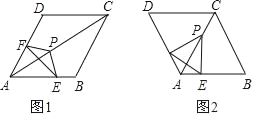
【題目】如圖1,菱形ABCD中,△EFP的頂點E、F、P分別在線段AB、AD、AC上,且EP=FP.
(1)證明:∠EPF+∠BAD=180°.
(2)若∠BAD=120°(如圖2),證明:AE+AF=AP.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖1,拋物線y=﹣![]() x2﹣
x2﹣![]() x+3與x軸交于A和B兩點(點A在點B的左側),與y軸相交于點C,點D的坐標是(0,﹣1),連接BC、AC
x+3與x軸交于A和B兩點(點A在點B的左側),與y軸相交于點C,點D的坐標是(0,﹣1),連接BC、AC
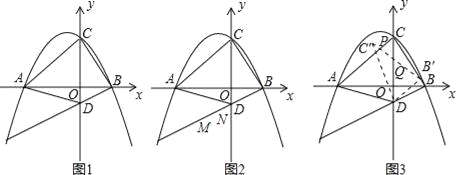
(1)求出直線AD的解析式;
(2)如圖2,若在直線AC上方的拋物線上有一點F,當△ADF的面積最大時,有一線段MN=![]() (點M在點N的左側)在直線BD上移動,首尾順次連接點A、M、N、F構成四邊形AMNF,請求出四邊形AMNF的周長最小時點N的橫坐標;
(點M在點N的左側)在直線BD上移動,首尾順次連接點A、M、N、F構成四邊形AMNF,請求出四邊形AMNF的周長最小時點N的橫坐標;
(3)如圖3,將△DBC繞點D逆時針旋轉α°(0<α°<180°),記旋轉中的△DBC為△DB′C′,若直線B′C′與直線AC交于點P,直線B′C′與直線DC交于點Q,當△CPQ是等腰三角形時,求CP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A在數軸上對應的數為x,點B對應的數為y,且點O為數軸上的原點,且![]() .
.
![]()
(1)點A對應的數為______;點B對應的數為______;線段![]() 的長度為_______;
的長度為_______;
(2)若數軸上有一點C,且![]() ,求點C在數軸上對應的數;
,求點C在數軸上對應的數;
(3)若點P從A點出發沿數軸的正方向以每秒2個單位的速度運動,同時Q點從B點出發沿數軸的負方向以每秒4個單位長度的速度運動,運動時間為t秒,當![]() 時,求t的值.
時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A,B,C,D為四家超市,其中超市D距A,B,C三家超市的路程分別為25km,10km,5km.現計劃在A,D之間的道路上建一個配貨中心P,為避免交通擁堵,配貨中心與超市之間的距離不少于2km.假設一輛貨車每天從P出發為這四家超市送貨各1次,由于貨車每次僅能給一家超市送貨,因此每次送貨后均要返回配貨中心P,重新裝貨后再前往其他超市.設P到A的路程為xkm,這輛貨車每天行駛的路程為ykm.
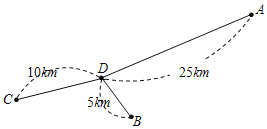
(1)求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)直接寫出配貨中心P建在什么位置,這輛貨車每天行駛的路程最短?最短路程是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC繞點A按順時針方向旋轉得到的.連接BE、CF相交于點D.
(1)求證:BE=CF.
(2)當四邊形ACDE為菱形時,求BD的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com