
【題目】某公司生產的一種商品其售價是成本的1.5倍,當售價降低5元時商品的利潤率為25%.若不進行任何推廣年銷售量為1萬件.為了獲得更好的利益,公司準備拿出一定的資金做推廣,根據經驗,每年投入的推廣費x萬元時銷售量y(萬件)是x的二次函數:當x為1萬元時,y是1.5(萬件).當x為2萬元時,y是1.8(萬件).
(1)求該商品每件的的成本與售價分別是多少元?
(2)求出年利潤與年推廣費x的函數關系式;
(3)如果投入的年推廣告費為1萬到3萬元(包括1萬和3萬元),問推廣費在什么范同內,公司獲得的年利潤隨推廣費的增大而增大?
【答案】(1)該商品每件的的成本與售價分別是20元、30元;(2)![]() ;(3)推廣費在1萬元到2.5萬元(包括1萬元和2.5萬元)時,公司獲得的年利潤隨推廣費的增大而增大.
;(3)推廣費在1萬元到2.5萬元(包括1萬元和2.5萬元)時,公司獲得的年利潤隨推廣費的增大而增大.
【解析】
(1)根據售價成本價=利潤,成本價乘以利潤率=利潤,列方程即可求解;
(2)根據每年投入的推廣費x萬元時銷售量y(萬件)是x的二次函數,代入所給數據即可求解;
(3)根據年利潤=單件利潤乘以銷售量再減去推廣費即可列出二次函數,根據二次函數的性質即可確定推廣費的取值范圍.
(1)設該商品每件的的成本為a元,則售價為元1.5a元,
根據題意,得
1.5a﹣5﹣a=25%a,
解得a=20,則1.5a=30,
答:該商品每件的的成本與售價分別是20元、30元.
(2)根據題意每年投入的推廣費x萬元時銷售量y(萬件)是x的二次函數,
設y=ax2+bx+c
∵不進行任何推廣年銷售量為1萬件,即當x=0時,y=1(萬件),
當x為1萬元時,y是1.5(萬件).當x為2萬元時,y是1.8(萬件).
∴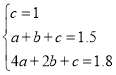
解得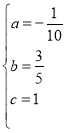
所以銷售量y與推廣費x的函數解析式為![]() .
.
所以設公司獲得的年利潤為w萬元,
答:年利潤與年推廣費x的函數關系式為w=10y=﹣x2+6x+10.
(3)公司獲得的年利潤為w萬元,根據題意,得
w=10y﹣x
=10(﹣![]() x2+
x2+![]() x+1)﹣x
x+1)﹣x
=﹣x2+5x+10
=﹣(x﹣![]() )2+
)2+![]()
∵1≤x≤3,
∴當1≤x≤2.5時,w隨x的增大而增大,
答:推廣費在1萬元到2.5萬元(包括1萬元和2.5萬元)時,公司獲得的年利潤隨推廣費的增大而增大.


科目:初中數學 來源: 題型:
【題目】(發現)如圖,點E,F分別在正方形ABCD的邊BC,CD上,連接EF.因為AB=AD,所以把ΔABE繞A逆時針旋轉90°至ΔADG,可使AB與AD重合.因為∠CDA=∠B=90°,所以∠FDG=180°,所以F、D、G共線.
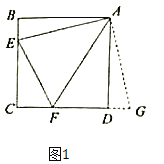
如果__________(填一個條件),可得ΔAEF≌ΔAGF.經過進一步研究我們可以發現:當BE,EF,FD滿足__________時,∠EAF=45°.
(應用)
如圖,在矩形ABCD中,AB=6,AD=m,點E在邊BC上,且BE=2.
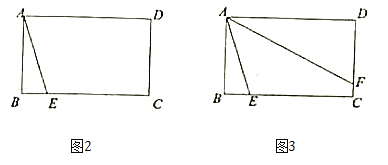
(1)若m=8,點F在邊DC上,且∠EAF=45°(如圖),求DF的長;
(2)若點F在邊DC上,且∠EAF=45°,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電視臺在它的娛樂性節目中每期抽出兩名場外幸運觀眾,有一期甲、乙兩人被抽為場外幸運觀眾,他們獲得了一次抽獎的機會,在如圖所示的翻獎牌的正面4個數字中任選一個,選中后翻開,可以得到該數字反面的獎品,第一個人選中的數字第二個人不能再選擇了.
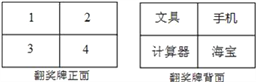
(1)如果甲先抽獎,那么甲獲得“手機”的概率是多少?
(2)小亮同學說:甲先抽獎,乙后抽獎,甲、乙兩人獲得“手機”的概率不同,且甲獲得“手機”的概率更大些.你同意小亮同學的說法嗎?為什么?請用列表或畫樹狀圖分析.
查看答案和解析>>
科目:初中數學 來源: 題型:
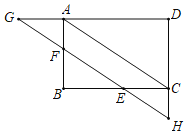
【題目】已知:如圖,在矩形ABCD中,E是邊BC上一點,過點E作對角線AC的平行線,交AB于F,交DA和DC的延長線于點G,H.
(1)求證:△AFG≌△CHE;
(2)若∠G=∠BAC,則四邊形ABCD是什么特殊四邊形?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=3,BC=4,將對角線AC繞對角線交點O旋轉,分別交邊AD、BC于點E、F,點P是邊DC上的一個動點,且保持DP=AE,連接PE、PF,設AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代數式表示)
(2)求△PEF面積的最小值;
(3)在運動過程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中考讓同學們感覺壓力較大,初三某班班主任想通過課間播放音樂來幫助學生緩解壓力,采用全面調查的方法調查了學生對音樂類型的興趣愛好,結果全班學生選擇集中在流行音樂、民族音樂、搖滾音樂和輕音樂四種音樂類型.根據調查的結果繪制成如圖所示的兩幅不完整的統計圖,請你根據圖中提供的信息解答下列問題:
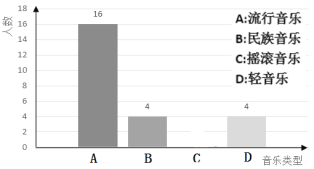
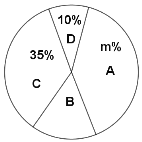
(1)求該班學生總人數,并把條形統計圖補充完整;
(2)求扇形統計圖中![]() 的值和表示流行音樂的扇形圓心角的度數;
的值和表示流行音樂的扇形圓心角的度數;
(3)班主任每天挑選出四種類型音樂各一首放在一個播放器內,每次隨機播放兩首不同音樂,請用畫樹狀圖或列表的方法求出某次恰好播放民族音樂和輕音樂的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現
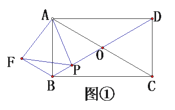
如圖①,矩形![]() 的對角線
的對角線![]() 交于點
交于點![]() ,且
,且![]() ,點
,點![]() 為線段
為線段![]() 上任意一點,以
上任意一點,以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,連接
,連接![]() ,則
,則![]() 與
與![]() 之間的數量關系是 ;
之間的數量關系是 ;
(2)類比延伸
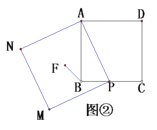
如圖②,在正方形![]() 中,點
中,點![]() 為
為![]() 邊上任意一點,以
邊上任意一點,以![]() 為邊作正方形
為邊作正方形![]() ,
,![]() 為正方形
為正方形![]() 的中心,連接
的中心,連接![]() ,直接寫出
,直接寫出![]() 與
與![]() 的數量關系為 ;
的數量關系為 ;
(3)拓展遷移
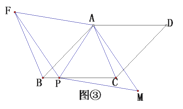
如圖③,在菱形![]() 中,
中,![]() ,點
,點![]() 為
為![]() 邊上一點,以
邊上一點,以![]() 為對角線作菱形
為對角線作菱形![]() ,滿足
,滿足![]() ,連接
,連接![]() ,猜想
,猜想![]() 與
與![]() 的數量關系,并證明你的結論.
的數量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位要將一份宣傳資料進行批量印刷.在甲印刷廠,在收取100元制版費的基礎上,每份收費0.5元;在乙印刷廠,在收取40元側版費的基礎上,每份收費0.7元.設該單位要印刷此宣傳資料![]() 份(
份(![]() 為正整數).
為正整數).
(Ⅰ)根據題意,填寫下表:
印劇數量(份) | 150 | 250 | 350 | 450 | … |
甲印刷廠收費(元) | 175 | ① | 275 | ② | … |
乙印刷廠收費(元) | 145 | 215 | ③ | 355 | … |
(Ⅱ)設在甲印刷廠收費![]() 元,在乙印刷廠收費
元,在乙印刷廠收費![]() 元,分別寫出
元,分別寫出![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(Ⅲ)當![]() 時,在哪家印刷廠花費少?請說明理由.
時,在哪家印刷廠花費少?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
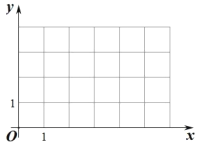
【題目】在平面直角坐標系![]() 中,我們把橫、縱坐標都是整數的點叫做整點,已知點
中,我們把橫、縱坐標都是整數的點叫做整點,已知點![]() ,點
,點![]() 是
是![]() 軸正半軸上的點,記
軸正半軸上的點,記![]() 內部(不包括邊界)的整點個數為
內部(不包括邊界)的整點個數為![]() ,當
,當![]() 時,點
時,點![]() 的橫坐標
的橫坐標![]() 的取值范圍是____.
的取值范圍是____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com