
【題目】一列快車從甲地勻速駛往乙地,一列慢車從乙地勻速駛往甲地,設先發出車輛行駛的時間為 xh , 兩車之間的距離為ykm,圖中的折線表示 y與x之間的函數關系。根據圖象回答下列問題:
(1)慢車的速度為________ km/h,快車的速度為__________km/h;
(2)求線段CD所表示的y與x之間的函數關系式,并寫出自變量 x的取值范圍;
(3)當 x取何值時,兩車之間的距離為300 km?

【答案】(1)80,120;(2) ![]() ;(3)1.2或4.2.
;(3)1.2或4.2.
【解析】整體分析:
(1)先利用前0.5小時的路程除以時間求出一輛車的速度,再利用相遇問題根據2.7小時列式求解即可得到另一輛車的速度;(2)理解點C和點D的意義,并求出它們的坐標,再求CD所在直線的函數關系式;(3)注意分類,兩車相遇前相距300km或兩車相遇后相距300km.
解:(1)(480-440)÷0.5=80km/h,
440÷(2.7-0.5)-80=120km/h,
所以慢車速度為80km/h,快車速度為120km/h;
故答案為80,120;
(2)因為快車走完全程所需時間為480÷120=4(h),
所以點D的橫坐標為4.5,
縱坐標為(120+80)×(4.5-2.7)=360,
即點D(4.5,360);
又點C(2.7,0).
設直線CD的解析式為y=kx+b,則
![]() ,解得
,解得![]() .
.
則y=200x-540,且2.7≤x≤4.5
所以線段CD所表示的y與x之間的函數關系式為y=200x-540,,自變量x的取值范圍是2.7≤x≤4.5.
(3)由題意,可知兩車行駛的過程中有2次兩車之間的距離為300km.
即(80+120)×(x-0.5)=440-300,解得x=1.2h;
或(80+120)×(x-2.7)=300,解得x=4.2h.
故x=1.2h或4.2h,兩車之間的距離為300km.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】如圖一條拋物線![]() (a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.
(a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.

(1)“拋物線三角形”一定是_______________三角形;
(2)若拋物線y=-x2+bx(b>0)的“拋物線三角形”是等腰直角三角形,求b的值;
(3)如圖,△OAB是拋物線y=-x2+b′x(b′>0)的“拋物線三角形”,是否存在以原點O為對稱中心的矩形ABCD?若存在,求出過O、C、D三點的拋物線的表達式;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點A,B,O,C為數軸上四點,點A對應數![]() ,點O對應0,點C對應3,
,點O對應0,點C對應3,![]() (AB表示點A到點B的距離).
(AB表示點A到點B的距離).

(1)填空:點C到原點O的距離______,點B對應的數______.(用含有a的式子)
(2)如圖2,將一刻度尺放在數軸上,刻度尺上“6cm”和“8.7cm”分別對應數軸上的點O和點C,若![]() ,求a的值和點A在刻度尺上對應的刻度。
,求a的值和點A在刻度尺上對應的刻度。
(3)如圖3,在(2)的條件下,點A以1單位長度/秒的速度向右運動,同時點C向左運動,若運動3秒時,點A和點C到原點O的距離相等,求點C的運動速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
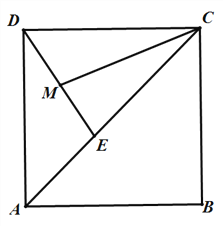
【題目】在菱形ABCD中,AC是對角線,CD=CE,連接DE,點M是線段DE的中點.
(1)如圖1,連接CM,若AC=16,CD=10,求DE的長
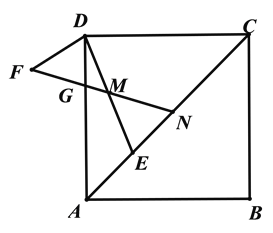
(2)如圖2,點F在菱形的外部,DF=DM,且∠CDA=∠FDE,連接FM交AD于點G,FM的延長線交AC于點N,求證:CN=AG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提升城市容貌,規范城市管理.我區城管某巡邏車在一條東西方向的公路上巡邏,規定向東為正,向西為負.某天,汽車從出發點開始所走的路程分別為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:千米).隊長要求匯報位置.
(單位:千米).隊長要求匯報位置.
(1)此時,駕駛員如何向隊長描述他的位置?
(2)如果隊長命令他馬上返回到出發點,這次巡邏(從出發點開始到最后又返回出發點)共耗油多少升?(已知每千米耗油![]() 升)
升)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對任意一個三位數![]() ,如果
,如果![]() 滿足各個數位上的數字互不相同,且都不為零,那么稱這個數為“相異數”,將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與111的商記為
滿足各個數位上的數字互不相同,且都不為零,那么稱這個數為“相異數”,將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與111的商記為![]() .例如
.例如![]() ,對調百位與十位上的數字得到213,對調百位與個位上的數字得到321,對調十位與個位上的數字得到132,這三個新三位數的和為213+321+132=666,666÷111=6,所以
,對調百位與十位上的數字得到213,對調百位與個位上的數字得到321,對調十位與個位上的數字得到132,這三個新三位數的和為213+321+132=666,666÷111=6,所以![]() .
.
(1)計算:![]() 和
和![]() ;
;
(2)若![]() 是“相異數”,證明:
是“相異數”,證明:![]() 等于
等于![]() 的各數位上的數字之和.
的各數位上的數字之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,平行四邊形ABCD,DE⊥AB.垂足E在BA的延長線上,BF⊥DC,垂足F在DC的延長線上.

(1)求證:四邊形BEDF是矩形;
(2)如圖2,若M、N分別為AD、BC的中點,連接EM、EN、FM、FN,求證:四邊形EMFN是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
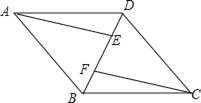
【題目】已知:如圖,四邊形ABCD是平行四邊形,AE∥CF,且分別交對角線BD于點E,F.
(1)求證:△AEB≌△CFD;
(2)連接AF,CE,若∠AFE=∠CFE,求證:四邊形AFCE是菱形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com