
【題目】在正方形![]() 中,
中,![]() 是一條對角線,點
是一條對角線,點![]() 在直線
在直線![]() 上(不與點
上(不與點![]() 、
、![]() 重合),連接
重合),連接![]() ,平移
,平移![]() ,使點
,使點![]() 移動到點
移動到點![]() ,得到
,得到![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,連接
,連接![]() ,
,![]() .
.
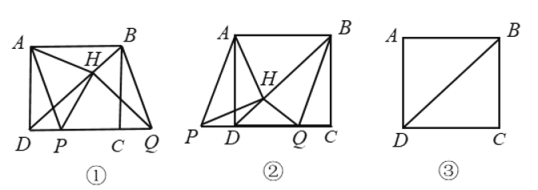
(問題發現)
(1)如圖①,若點![]() 在線段
在線段![]() 上,
上,![]() 與
與![]() 的數量關系是________,位置關系是________.
的數量關系是________,位置關系是________.
(拓展探究)
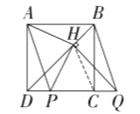
(2)如圖②,若點![]() 在線段
在線段![]() 的延長線上,其他條件不變,(1)中的結論是否仍然成立?若成立,請給出證明,否則說明理由.
的延長線上,其他條件不變,(1)中的結論是否仍然成立?若成立,請給出證明,否則說明理由.
(解決問題)
(3)若點![]() 在線段
在線段![]() 的延長線上,且
的延長線上,且![]() ,正方形
,正方形![]() 的邊長為2,請直接寫出求
的邊長為2,請直接寫出求![]() 的長度.
的長度.
【答案】(1)![]() ,
,![]() ;(2)結論仍然成立,理由見解析;(3)
;(2)結論仍然成立,理由見解析;(3)![]() .
.
【解析】
(1)連接HC,根據正方形的性質、等腰直角三角形的性質得到△HDP≌△HQC,根據全等三角形的性質得到HP=HC,∠DHP=∠QHC,根據正方形是軸對稱圖形證明結論;
(2)同(1)的證明方法相同,根據圖形證明即可;
(3)由(1)的結論AH=PH,AH⊥PH,得出∠HPA=45°,推導出∠APD=30°,再由三角函數即可求解.
(1)![]() ,
,![]() .
.
證明如下:如解圖,連接![]() ,
,
∵四邊形![]() 是正方形,
是正方形,
∴∠![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
由平移的性質可知![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
根據正方形是軸對稱圖形得到![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,![]() .
.
故答案為:![]() ,
,![]() ;
;
(2)(1)中的結論仍然成立,
理由如下:如解圖,連接![]() ,
,

∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
由平移的性質可知![]() ,
,
在![]() 和
和![]() 中,
中,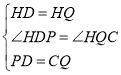 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
根據正方形是軸對稱圖形得到![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(3)![]() .
.
由(1)知,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線L:y=ax2+bx+c與x軸交于A、B(3,0)兩點(A在B的左側),與y軸交于點C(0,3),已知對稱軸x=1.
(1)求拋物線L的解析式;
(2)將拋物線L向下平移h個單位長度,使平移后所得拋物線的頂點落在△OBC內(包括△OBC的邊界),求h的取值范圍;
(3)設點P是拋物線L上任一點,點Q在直線l:x=﹣3上,△PBQ能否成為以點P為直角頂點的等腰直角三角形?若能,求出符合條件的點P的坐標;若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形紙片ABCD,怎樣折疊,能使邊AB被三等分?
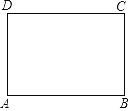
以下是小紅的研究過程.
思考過程 | 要使邊AB被三等分,若從邊DC上考慮,就是要折出DM= 也就是要折出DM= 當DB、AM相交于F時,即要折出對角線上的DF= |
折疊方法和示意圖 | ①折出DB;對折紙片,使D、B重合,得到的折痕與DB相交于點E;繼續折疊紙片,使D、B與E重合,得到的折痕與DB分別相交于點F、G; ②折出AF、CG,分別交邊CD、AB于M、Q; ③過M折紙片,使D落在MC上,得到折痕MN,則邊AB被N、Q三等分.
|
(1)整理小紅的研究過程,說明AN=NQ=QB;
(2)用一種與小紅不同的方法折疊,使邊AB被三等分.(需簡述折疊方法并畫出示意圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
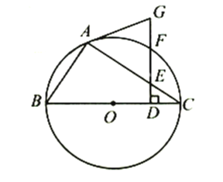
【題目】如圖,![]() 為⊙
為⊙![]() 的內接三角形,
的內接三角形,![]() 為⊙
為⊙![]() 的直徑,在線段
的直徑,在線段![]() 上取點
上取點![]() (不與端點重合),作
(不與端點重合),作![]() ,分別交
,分別交![]() 、圓周于
、圓周于![]() 、
、![]() ,連接
,連接![]() ,已知
,已知![]() .
.
(1)求證:![]() 為⊙
為⊙![]() 的切線;
的切線;
(2)已知![]() ,填空:
,填空:
①當![]() __________
__________![]() 時,四邊形
時,四邊形![]() 是菱形;
是菱形;
②若![]() ,當
,當![]() __________時,
__________時,![]() 為等腰直角三角形.
為等腰直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的函數圖象如圖,點
的函數圖象如圖,點![]() 位于坐標原點,點
位于坐標原點,點![]() 在
在![]() 軸的正半軸上,點
軸的正半軸上,點![]() 在二次函數
在二次函數![]() 位于第一象限的圖象上,
位于第一象限的圖象上,![]() ,
,![]() ,
,![]() ,
,![]() …都是直角頂點在拋物線上的等腰直角三角形,則
…都是直角頂點在拋物線上的等腰直角三角形,則![]() 的斜邊長為( )
的斜邊長為( )

A.20B.![]() C.22D.
C.22D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年春季開學后,某校制定了《新冠肺炎疫情防控期間就餐規范》,條例規定:不對面就餐、食而不語、錯峰就餐、鼓勵打包等就餐措施.為了解學生對規范的認知程度,校園小記者隨機調查部分同學,并根據調查結果繪制了如下兩幅不完整的統計圖表:

請根據以上圖表,解答下列問題:
(1)這次被調查的同學共有______人,![]() ______,
______,![]() ______;
______;
(2)求扇形統計圖中B部分所對圓心角度數;
(3)學校團委及政教處準備對“不太了解”及“毫不知情”的同學進行再學習培訓,請問我校2400名學生中預計有多少人要接受再學習?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣教育局為了豐富初中學生的大課間活動,要求各學校開展形式多樣的陽光體育活動.某中學就“學生體育活動興趣愛好”的問題,隨機調查了本校某班的學生,并根據調查結果繪制成如下的不完整的扇形統計圖和條形統計圖:
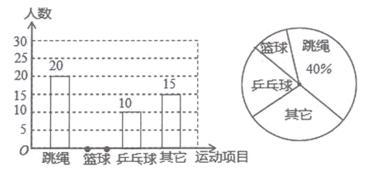
(1)在這次調查中,共調查了 人,在扇形統計圖中,“乒乓球”的百分比為 %,如果學校有800名學生,估計全校學生中有 人喜歡籃球項目;
(2)請將條形統計圖補充完整;
(3)學校在喜歡籃球的初一學生中挑選了3名同學,分別是李明、林海和陳陽,然后在這3名學生中最終挑選2人參加學校的籃球隊,請用列表法或畫樹狀圖的方法求出李明最終被選上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形![]() 中,點
中,點![]() 為對角線
為對角線![]() 上一動點(點
上一動點(點![]() 與點
與點![]() 、
、![]() 不重合),連接
不重合),連接![]() ,作
,作![]() 交射線
交射線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() 、
、![]() ,作射線
,作射線![]() 交射線
交射線![]() 于點
于點![]()
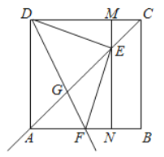
(1)求證:![]() ;
;
(2)當![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com