
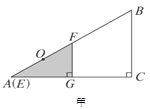
【題目】如圖甲,有兩個形狀完全相同的直角三角形ABC和EFG疊放在一起(點A與點E重合),已知AC![]() 8 cm,BC
8 cm,BC![]() 6 cm,∠C
6 cm,∠C![]() 90°,EG
90°,EG![]() 4 cm,∠EGF
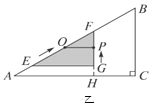
4 cm,∠EGF![]() 90°,O是△EFG斜邊上的中點. 如圖乙,若整個△EFG從圖甲的位置出發,以1 cm/s的速度沿射線AB方向平移,在△EFG平移的同時,點P從△EFG的頂點G出發,以1 cm/s的速度在直角邊GF上向點F運動,當點P到達點F時,點P停止運動,△EFG也隨之停止平移. 設運動時間為x(s),FG的延長線交AC于H,四邊形OAHP的面積為y(cm2)(提示:不考慮點P與G、F重合的情況).
90°,O是△EFG斜邊上的中點. 如圖乙,若整個△EFG從圖甲的位置出發,以1 cm/s的速度沿射線AB方向平移,在△EFG平移的同時,點P從△EFG的頂點G出發,以1 cm/s的速度在直角邊GF上向點F運動,當點P到達點F時,點P停止運動,△EFG也隨之停止平移. 設運動時間為x(s),FG的延長線交AC于H,四邊形OAHP的面積為y(cm2)(提示:不考慮點P與G、F重合的情況).
(1)當x為何值時,OP∥AC?
(2)求y與x之間的函數關系式,并確定自變量x的取值范圍;
(3)是否存在某一時刻,使四邊形OAHP面積與△ABC面積的比為![]() ?若存在,求出x的值;若不存在,說明理由.
?若存在,求出x的值;若不存在,說明理由.
【答案】(1)當x為1.5 s時,OP∥AC;(2)![]() +3 (0<x<3);(3)x1=
+3 (0<x<3);(3)x1=![]()
【解析】分析:(1)由于O是EF中點,因此當P為FG的中點時,OP∥EG∥AC,據此可求出x的值.
(2)由于四邊形AHPO形狀不規則,可根據S四邊形OAHP=S△AFH![]() S△OFP,
S△OFP, ![]() 中,AH的長可用AF的長和∠FAH的余弦值求出,同理可求出FH的表達式(也可用相似三角形來得出AH、FH的長).
中,AH的長可用AF的長和∠FAH的余弦值求出,同理可求出FH的表達式(也可用相似三角形來得出AH、FH的長).![]() 中,過點O作OD⊥FP,垂足為D.PF的長易知,而OD的長,可根據OF的長和∠FOD的余弦值得出.由此可求得y、x的函數關系式.
中,過點O作OD⊥FP,垂足為D.PF的長易知,而OD的長,可根據OF的長和∠FOD的余弦值得出.由此可求得y、x的函數關系式.
(3)先求出四邊形OAHP面積與△ABC,然后將其代入(2)的函數式中即可得出x的值.
詳解:(1)∵Rt△EFG∽Rt△ABC,∴![]() .
.
∴FG=![]() =3 cm.
=3 cm.
∵當P為FG的中點時,OP∥EG,EG∥AC,
∴OP∥AC.
∴x=![]() ×3=1.5(s).
×3=1.5(s).
∴當x為1.5 s時,OP∥AC.
(2)在Rt△EFG中,由勾股定理得EF=5 cm.
∵EG∥AH,∴△EFG∽△AFH.
∴![]() ,即
,即![]() .
.
∴AH=![]() (x+5),FH=
(x+5),FH=![]() (x+5).
(x+5).
過點O作OD⊥FP,垂足為D.
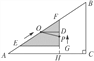
∵點O為EF中點,∴OD=![]() EG=2 cm.
EG=2 cm.
∵FP=![]() ,
,
∴S四邊形OAHP=S△AFH![]() S△OFP
S△OFP![]()
![]() AH·FH
AH·FH![]()
![]() OD·FP
OD·FP
=![]() ×
×![]() (x+5) ×
(x+5) ×![]() (x+5)
(x+5)![]()
![]() ×2×(3
×2×(3![]() x)
x)
=![]() +3 (0<x<3).
+3 (0<x<3).
(3)假設存在某一時刻x,使得四邊形OAHP面積與△ABC面積的比為13∶24,
則S四邊形OAHP![]()
![]() ×S△ABC.
×S△ABC.
∴![]() ×
×![]() ×6×8.
×6×8.
∴6x2![]() 85x
85x![]() 250
250![]() 0.
0.
解得x1=![]() ,x2=
,x2=![]()
![]() (舍去).
(舍去).
當x=![]() (s)時,四邊形OAHP面積與△ABC面積的比為13:24.
(s)時,四邊形OAHP面積與△ABC面積的比為13:24.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
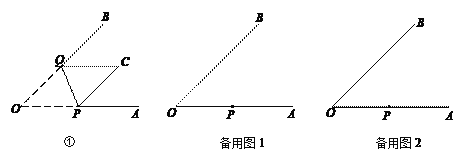
【題目】圖①是一張∠AOB=45°的紙片折疊后的圖形,P、Q分別是邊OA、OB上的點,且OP=2 cm.將∠AOB沿PQ折疊,點O落在紙片所在平面內的C處.
(1)①當PC∥QB時,OQ= cm;
②在OB上找一點Q,使PC⊥QB(尺規作圖,保留作圖痕跡);
(2)當折疊后重疊部分為等腰三角形時,求OQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“美化城市,改善人民居住環境”是城市建設的一項重要內容.北京市將重點圍繞城市副中心、大興國際機場、冬奧會、世園會、永定河、溫榆河、南中軸等重要節點區域綠化,到2022年,全市將真正形成一片集“萬畝城市森林、百萬喬灌樹木、百種鄉土植物、二十四節氣林窗、四季景觀大道”于一體的城市森林.2018年當年計劃新增造林23萬畝,2019年計劃新增造林面積大體相當于27.8個奧森公園的面積,預計2020年計劃新增造林面積達到38.87萬畝,求2018年至2020年計劃新增造林面積的年平均增長率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點![]() 為原點,點
為原點,點![]() 表示的數為
表示的數為![]() ,點
,點![]() 表示的數為
表示的數為![]() ,且
,且![]() 滿足
滿足![]()
(1)A、B兩點對應的數分別為![]() _____,
_____,![]() ______;
______;
(2)若將數軸折疊,使得![]() 點與
點與![]() 點重合,則原點
點重合,則原點![]() 與數______表示的點重合.
與數______表示的點重合.
(3)若點A、B分別以4個單位/秒和2個單位/秒的速度相向而行,則幾秒后A、B兩點相距2個單位長度?
(4)若點A、B以(3)中的速度同時向右運動,點![]() 從原點
從原點![]() 以7個單位/秒的速度向右運動,設運動時間為
以7個單位/秒的速度向右運動,設運動時間為![]() 秒,請問:在運動過程中,
秒,請問:在運動過程中,![]() 的值是否會發生變化?若變化,請用
的值是否會發生變化?若變化,請用![]() 表示這個值;若不變,請求出這個定值.
表示這個值;若不變,請求出這個定值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 和
和![]() 有一條公共邊
有一條公共邊![]() ,且
,且![]() ,
,![]() 是
是![]() 的平分線,
的平分線,![]() 是
是![]() 的平分線.
的平分線.
(1)畫出圖形;
(2)若![]() ,
,![]() ,求
,求![]() 的大小;
的大小;
(3)通過對以上的解題回顧,你發現![]() 與
與![]() 、
、![]() 三個角之間有怎樣的大小關系?請把你的發現結論直接寫出來.
三個角之間有怎樣的大小關系?請把你的發現結論直接寫出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點![]() 在線段
在線段![]() 上,圖中共有三條線段
上,圖中共有三條線段![]() ,
,![]() 和
和![]() ,若其中有一條線段的長度是另外一條線段長度的2倍,則稱點
,若其中有一條線段的長度是另外一條線段長度的2倍,則稱點![]() 是線段
是線段![]() 的“巧點”.
的“巧點”.
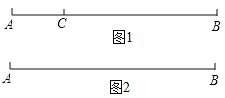
(1)線段的中點_________這條線段的“巧點”;(填“是”或“不是”);
(2)如圖2,已知![]() .動點
.動點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 勻速運動;點
勻速運動;點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 向點
向點![]() 勻速運動,點
勻速運動,點![]() ,
,![]() 同時出發,當其中一點到達終點時,運動停止.設移動的時間為
同時出發,當其中一點到達終點時,運動停止.設移動的時間為![]() ,當
,當![]() _________
_________![]() 時,
時,![]() 為
為![]() 的“巧點”.
的“巧點”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種產品形狀是長方體,長為8cm,它的展開圖如圖:
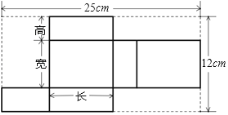
(1)求該長方體的寬和高;
(2)請為廠家設計一種包裝紙箱,使每箱能裝2件這種產品,要求沒有空隙且要使該紙箱所用材料盡可能少(紙箱的表面積盡可能小),并求出該紙箱的體積。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三位運動員在相同條件下各射靶10次,每次射靶的成績如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根據以上數據完成下表:
平均數 | 中位數 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依據表中數據分析,哪位運動員的成績最穩定,并簡要說明理由;
(3)比賽時三人依次出場,順序由抽簽方式決定.求甲、乙相鄰出場的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數按要求分類
+8.3,-4,-0.8,-![]() ,0,π,90,-|-24|,15%,
,0,π,90,-|-24|,15%,![]() 中,
中,
負數有______________________________,
分數有______________________________.
整數有______________________________.
有理數有______________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com