
【題目】如圖,已知拋物線經y=ax2+bx﹣3過A(1,0)、B(3,0)、C三點.

(1)求拋物線解析式;
(2)如圖1,點P是BC上方拋物線上一點,作PQ∥y軸交BC于Q點.請問是否存在點P使得△BPQ為等腰三角形?若存在,請直接寫出P點坐標;若不存在,請說明理由;
(3)如圖2,連接AC,點D是線段AB上一點,作DE∥BC交AC于E點,連接BE.若△BDE∽△CEB,求D點坐標.
【答案】(1)y=﹣x2+4x﹣3;(2)存在點P使得△BPQ為等腰三角形,P點坐標為P1(1,0),P2(2,1),![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用待定系數法求解可得拋物線的表達式;
(2)先求出直線![]() 的解析式,分三種情況:當
的解析式,分三種情況:當![]() 時,設
時,設![]() ,可表示出三條線段長,則解方程可求出P點坐標;
,可表示出三條線段長,則解方程可求出P點坐標;
(3)證得![]() 可得比例線段求出AE長,當
可得比例線段求出AE長,當![]() 時可求出D點坐標.
時可求出D點坐標.
(1)將![]() 代入
代入![]() 得:
得:![]() ,
,
解得![]() ,
,
拋物線解析式![]() ;
;
(2)存在點P使得△BPQ為等腰三角形,
∵B(3,0),C(0,﹣3),
∴設直線BC的解析式為![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴直線BC的解析式為![]() ,
,
設![]() ,則
,則![]() ,可分三種情況考慮:
,可分三種情況考慮:
①當![]() 時,由題意得P、Q關于x軸對稱,
時,由題意得P、Q關于x軸對稱,
∴![]() ,
,
解得:![]() (舍去),
(舍去),
∴![]() ,
,
②當![]() 時,
時,![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
③當![]() 時,有
時,有![]() ,
,
整理得:![]() ,
,
解得![]() .
.
∴![]() .
.
綜合以上可得P點坐標為P1(1,0),P2(2,1),![]() ;
;
(3)∵△BDE∽△CEB,
∴∠ABE=∠ACB,
∵∠BAE=∠CAB,
∴△ABE∽△ACB,
又∵![]() ,
,
∴![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴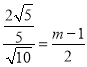
∴![]()
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】學校運動會的立定跳遠和1分鐘跳繩兩個單項比賽分成預賽和決賽兩個階段.下表為參加這兩項比賽的10名學生的預賽成績:
學生編號 成績 項目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳遠(單位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分鐘跳繩(單位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在這10名學生中,同時進入兩項決賽的只有6人,進入立定跳遠決賽的有8![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩人在相同條件下完成了10次射擊訓練,兩人的成績如圖所示。

根據以上信息,整理分析數據如下:
平均成績/環 | 中位數/環 | 方差/環 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根據訓練成績,你認為選派哪一名隊員參賽更好?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋里裝有分別標有數字-3、-1、0、2的四個小球,除數字不同外,小球沒有任何區別,每次試驗先攪拌均勻.
(1)從中任取一球,將球上的數字記為a,則關于x的元二次方程x2-2x-a+1=0有實數根的概率______;
(2)從中任取一球,將球上的數字作為點的橫坐標,記為x(不放回);再任取一球,將球上的數字作為點的縱坐標,記為y,試用畫樹狀圖(或列表法)表示出點(x,y)所有可能出現的結果,并求點(x,y)落在第三象限內的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等邊三角形,點D在邊AB上.

(1)如圖1,當點E在邊BC上時,求證DE=EB;
(2)如圖2,當點E在△ABC內部時,猜想ED和EB數量關系,并加以證明;
(3)如圖3,當點E在△ABC外部時,EH⊥AB于點H,過點E作GE∥AB,交線段AC的延長線于點G,AG=5CG,BH=3.求CG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為實現區域教育均衡發展,我市計劃對某縣A、B兩類薄弱學校全部進行改造.根據預算,共需資金1555萬元改造一所A類學校和兩所B類學校共需資金230萬元;改造兩所A類學校和一所B類學校共需資金205萬元
(1)改造一所A類學校和一所B類學校所需的資金分別是多少萬元?
(2)根據我市教育局規劃計劃今年對該縣A、B兩類學校進行改造,要求改造的A類學校是B類學校的2倍多2所,在計劃投入資金不超過1555萬元的條件下,至多能改造多少所A類學校?
查看答案和解析>>
科目:初中數學 來源: 題型:
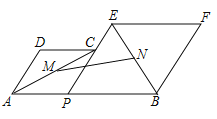
【題目】如圖,已知![]() ,
,![]() 為線段
為線段![]() 上的一個動點,分別以
上的一個動點,分別以![]() ,
,![]() 為邊在
為邊在![]() 的同側作菱形
的同側作菱形![]() 和菱形
和菱形![]() .點
.點![]() ,
,![]() ,
,![]() 在一條直線上,
在一條直線上,![]() ,
,![]() 、
、![]() 分別是對角線
分別是對角線![]() 、
、![]() 的中點.當點
的中點.當點![]() 在線段
在線段![]() 上移動時,點
上移動時,點![]() 、
、![]() 之間的距離最短為_______.
之間的距離最短為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校餐廳中,一張桌子可坐6人,現有以下兩種擺放方式:
(1)當有5張桌子時,第一種方式能坐 人,第二種方式能坐 人.
(2)當有n張桌子時,第一種方式能坐 人,第二種方式能坐 人.
(3)新學期有200人在學校就餐,但餐廳只有60張這樣的餐桌,若你是老師,你打算選擇以下哪種方式來擺放餐桌?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() 點
點![]() 與點
與點![]() 在
在![]() 的同側,且
的同側,且![]() .
.

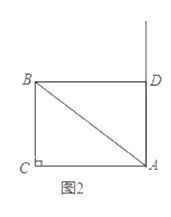
(1)如圖1,點![]() 不與點
不與點![]() 重合,連結
重合,連結![]() 交
交![]() 于點
于點![]() .設
.設![]() 求
求![]() 關于
關于![]() 的函數解析式,寫出自變量
的函數解析式,寫出自變量![]() 的取值范圍;
的取值范圍;
(2)是否存在點![]() ,使
,使![]() 與
與![]() 相似,若存在,求
相似,若存在,求![]() 的長;若不存在,請說明理由;
的長;若不存在,請說明理由;
(3)如圖2,過點![]() 作
作![]() 垂足為
垂足為![]() .將以點
.將以點![]() 為圓心,
為圓心,![]() 為半徑的圓記為
為半徑的圓記為![]() .若點
.若點![]() 到
到![]() 上點的距離的最小值為
上點的距離的最小值為![]() ,求
,求![]() 的半徑.
的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com