
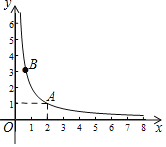
【題目】如圖,在平面直角坐標系![]() 中的第一象限內,反比例函數圖象過點
中的第一象限內,反比例函數圖象過點![]() 和另一動點
和另一動點![]() .
.
(1)求此函數表達式;
(2)如果![]() ,寫出
,寫出![]() 的取值范圍;
的取值范圍;
(3)直線![]() 與坐標軸交于點
與坐標軸交于點![]() ,如果
,如果![]() ,直接寫出點
,直接寫出點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)點
;(3)點![]() 的坐標為(0,3)或(6,0).
的坐標為(0,3)或(6,0).
【解析】
(1)由點![]() 的坐標,利用待定系數法即可求出反比例函數表達式;
的坐標,利用待定系數法即可求出反比例函數表達式;
(2)求![]() 時x的取值范圍就是求A點上方的函數圖象對應的x的取值范圍,據圖寫出即可;
時x的取值范圍就是求A點上方的函數圖象對應的x的取值范圍,據圖寫出即可;
(3)分點![]() 在點
在點![]() 的左側和右側考慮,構造圖形,利用三角形的中位線即可求出點
的左側和右側考慮,構造圖形,利用三角形的中位線即可求出點![]() 的坐標.
的坐標.
解:(1)設反比例函數表達式為![]() ,
,
∵此函數過![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴此函數表達式是![]() .
.
(2)∵點![]() 在反比例函數
在反比例函數![]() 的第一象限的圖象上,∴
的第一象限的圖象上,∴![]() ,且
,且![]() ,
,
∵![]() ,∴
,∴![]() .
.
(3)當點![]() 在點
在點![]() 左邊時,分別過點
左邊時,分別過點![]() 、
、![]() 作
作![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() 、
、![]() ,如圖1所示.
,如圖1所示.
∵![]() ,
,![]() ,∴
,∴![]() 為
為![]() 的中位線,
的中位線,
∴![]() ,∴點
,∴點![]() 的坐標為
的坐標為![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴點![]() ;
;
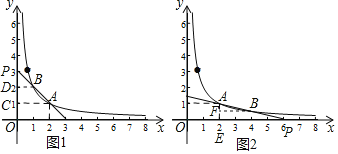
當點![]() 在點
在點![]() 的右邊時,過點
的右邊時,過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則
,則![]() 為
為![]() 的中位線,如圖2所示.
的中位線,如圖2所示.
∴![]() ,∴點
,∴點![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴點![]() .
.
綜上所述:點![]() 的坐標為(0,3)或(6,0).
的坐標為(0,3)或(6,0).


科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD外取一點E,連接AE、BE、DE.過點A作AE的垂線交DE于點P.若AE=AP=1,PB=![]() .下列結論:①△APD≌△AEB;②點B到直線AE的距離為
.下列結論:①△APD≌△AEB;②點B到直線AE的距離為![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正確結論的序號是 .
.其中正確結論的序號是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠ACB=90°,點D是邊AB的中點,點E在邊BC上,AE=BE,點M是AE的中點,聯結CM,點G在線段CM上,作∠GDN=∠AEB交邊BC于N.

(1)如圖2,當點G和點M重合時,求證:四邊形DMEN是菱形;
(2)如圖1,當點G和點M、C不重合時,求證:DG=DN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣![]() x2﹣x+4與x軸交于A,B兩點(A在B的左側),與y軸交于點C.
x2﹣x+4與x軸交于A,B兩點(A在B的左側),與y軸交于點C.
(1)求點A,點B的坐標;
(2)P為第二象限拋物線上的一個動點,求△ACP面積的最大值.
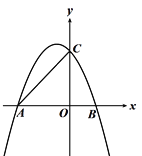
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知![]() ,
,![]() ,點P為AB邊上的一個動點,點E、F分別是CA,CB邊的中點,過點P作
,點P為AB邊上的一個動點,點E、F分別是CA,CB邊的中點,過點P作![]() 于D,設
于D,設![]() ,圖中某條線段的長為y,如果表示y與x的函數關系的大致圖象如圖2所示,那么這條線段可能是
,圖中某條線段的長為y,如果表示y與x的函數關系的大致圖象如圖2所示,那么這條線段可能是![]()
![]()
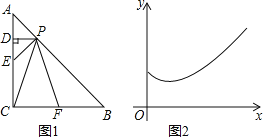
A. PDB. PEC. PCD. PF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們給出如下定義:兩個圖形![]() 和
和![]() ,在
,在![]() 上的任意一點
上的任意一點![]() 引出兩條垂直的射線與
引出兩條垂直的射線與![]() 相交于點
相交于點![]() 、
、![]() ,如果
,如果![]() ,我們就稱
,我們就稱![]() 、
、![]() 為點
為點![]() 的垂等點,
的垂等點,![]() 、
、![]() 為點
為點![]() 的垂等線段,點
的垂等線段,點![]() 為垂等射點.
為垂等射點.
(1)如圖1,在平面直角坐標系![]() 中,點
中,點![]() 為
為![]() 軸上的垂等射點,過
軸上的垂等射點,過![]() 作
作![]() 軸的平行線
軸的平行線![]() ,則直線
,則直線![]() 上的
上的![]() 為點
為點![]() 的垂等點的是_______;
的垂等點的是_______;
(2)如果一次函數圖象過![]() ,點
,點![]() 為垂等射點
為垂等射點![]() 的一個垂等點且另一個垂等點
的一個垂等點且另一個垂等點![]() 也在此一次函數圖象上,在圖2中畫出示意圖并寫出一次函數表達式;
也在此一次函數圖象上,在圖2中畫出示意圖并寫出一次函數表達式;
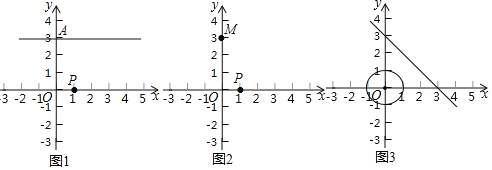
(3)如圖3,以點![]() 為圓心,1為半徑作
為圓心,1為半徑作![]() ,垂等射點
,垂等射點![]() 在
在![]() 上,垂等點在經過(3,0),(0,3)的直線上,如果關于點
上,垂等點在經過(3,0),(0,3)的直線上,如果關于點![]() 的垂等線段始終存在,求垂等線段
的垂等線段始終存在,求垂等線段![]() 長的取值范圍(畫出圖形直接寫出答案即可).
長的取值范圍(畫出圖形直接寫出答案即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是
是![]() 的函數,如表是
的函數,如表是![]() 與
與![]() 的幾組對應值.
的幾組對應值.
| … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小明根據學習函數的經驗,利用上述表格所反映出的![]() 與
與![]() 之間的變化規律,對該函數的圖象與性質進行了探究.
之間的變化規律,對該函數的圖象與性質進行了探究.
下面是小明的探究過程,請補充完整:

(1)如圖,在平面直角坐標系![]() 中,描出了以上表中各對對應值為坐標的點.根據描出的點,畫出該函數的圖象;
中,描出了以上表中各對對應值為坐標的點.根據描出的點,畫出該函數的圖象;
(2)根據畫出的函數圖象,寫出:
①![]() 對應的函數值
對應的函數值![]() 約為 ;
約為 ;
②該函數的一條性質: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系xOy中,二次函數![]()
![]() 的圖像與x軸交于點A、B(點A在點B的左側),與y軸交于點C,△ABC的面積為12.
的圖像與x軸交于點A、B(點A在點B的左側),與y軸交于點C,△ABC的面積為12.
(1)求這個二次函數的解析式;
(2)點D的坐標為![]() ,點P在二次函數的圖像上,∠ADP為銳角,且
,點P在二次函數的圖像上,∠ADP為銳角,且![]() ,請直接寫出點P的橫坐標;
,請直接寫出點P的橫坐標;
(3)點E在x軸的正半軸上,![]() ,點O與點
,點O與點![]() 關于EC所在直線對稱,過點O作
關于EC所在直線對稱,過點O作![]() 的垂線,垂足為點N,ON與EC交于點M.若
的垂線,垂足為點N,ON與EC交于點M.若![]() ,求點E的坐標.
,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2022年將在北京﹣﹣張家口舉辦冬季奧運會,北京將成為世界上第一個既舉辦夏季奧運會,又舉辦冬季奧運會的城市,某校開設了冰球選修課,12名同學被分成甲、乙兩組進行訓練,他們的身高(單位:cm)如表所示:
隊員1 | 隊員1 | 隊員1 | 隊員1 | 隊員1 | 隊員1 | |
甲組 | 176 | 177 | 175 | 176 | 177 | 175 |
乙組 | 178 | 175 | 170 | 174 | 183 | 176 |
設兩隊隊員身高的平均數依次為![]() ,
,![]() ,方差依次為
,方差依次為![]() ,
,![]() ,下列關系中正確的是( )
,下列關系中正確的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,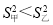 D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com