
【題目】如圖,在△ABC中,AB=AC,BE平分∠ABC交AC于點E,過點E作EF∥BC交AB于點F,D是BC邊上的中點,連結(jié)AD.

(1)若∠BAD=55°,求∠C的度數(shù);
(2)猜想FB與FE的數(shù)量關(guān)系,并證明你的猜想.
【答案】(1)35°;(2)FB=FE,證明見解析.
【解析】
(1)利用等腰三角形的三線合一的性質(zhì)可得∠ADB=90°,再利用直角三角形的性質(zhì)求出∠ABC,然后根據(jù)等腰三角形的性質(zhì)即可求得結(jié)果;
(2)猜想FB=FE,利用角平分線的性質(zhì)和平行線的性質(zhì)可得∠FBE=∠FEB,再利用等腰三角形的判定方法即可證明猜想.
(1)解:∵AB=AC,∴∠C=∠ABC,
∵BD=CD,AB=AC,∴AD⊥BC,∴∠ADB=90°,
∵∠BAD=55°,∴∠C=∠ABC=90°﹣55°=35°;
(2)猜想:FB=FE.
證明:∵BE平分∠ABC,∴∠ABE=∠CBE,
∵EF∥BC,∴∠FEB=∠CBE,
∴∠FBE=∠FEB,
∴FB=FE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:
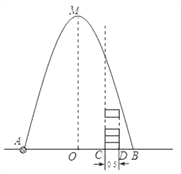
【題目】如圖,在水平地面點A處有一網(wǎng)球發(fā)射器向空中發(fā)射網(wǎng)球,網(wǎng)球飛行路線是一條拋物線,在地面上落點為B,有人在直線AB上點C(靠點B一側(cè))豎直向上擺放若干個無蓋的圓柱形桶.試圖讓網(wǎng)球落入桶內(nèi),已知AB=4米,AC=3米,網(wǎng)球飛行最大高度OM=5米,圓柱形桶的直徑為0.5米,高為0.3米(網(wǎng)球的體積和圓柱形桶的厚度忽略不計).當(dāng)豎直擺放圓柱形桶至少________個時,網(wǎng)球可以落入桶內(nèi).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某氣球內(nèi)充滿一定質(zhì)量的氣體,當(dāng)溫度不變時,氣球內(nèi)氣體的氣壓p(kPa)是氣體體積V(m3)的反比例函數(shù),其圖象如圖所示.

(1)寫出這一函數(shù)的表達(dá)式.
(2)當(dāng)氣體體積為1 m3時,氣壓是多少?
(3)當(dāng)氣球內(nèi)的氣壓大于140 kPa時,氣球?qū)⒈?/span>,為了安全考慮,氣體的體積應(yīng)不小于多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】二次函數(shù)圖象如圖所示,對稱軸為![]() ,給出下列結(jié)論:①
,給出下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正確的結(jié)論有( )
,其中正確的結(jié)論有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AD是△ABC的高線,BD=CD,點E是AD上一點,BE=BC,將△ABE沿BE所在直線折疊,點A落在點A′位置上,連接AA',BA′,EA′與AC相交于點H,BA′與AC相交于點F.小夏依據(jù)上述條件,寫出下列四個結(jié)論:①∠EBC=60°;②∠BFC=60°;③∠EA′A=60°;④∠A′HA=60°.以上結(jié)論中,正確的是( )

A.①B.③④C.①②③D.①②④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 紙板中,
紙板中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一點,過點
上一點,過點![]() 沿直線剪下一個與
沿直線剪下一個與![]() 相似的小三角形紙板,如果有
相似的小三角形紙板,如果有![]() 種不同的剪法,那么
種不同的剪法,那么![]() 長的取值范圍是________.
長的取值范圍是________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知矩形![]() 的邊長
的邊長![]() .某一時刻,動點
.某一時刻,動點![]() 從
從![]() 點出發(fā)沿
點出發(fā)沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 點勻速運動;同時,動點
點勻速運動;同時,動點![]() 從
從![]() 點出發(fā)沿
點出發(fā)沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 點勻速運動,問:
點勻速運動,問:

(1)經(jīng)過多少時間,![]() 的面積等于矩形
的面積等于矩形![]() 面積的
面積的![]() ?
?
(2)是否存在時刻t,使以A,M,N為頂點的三角形與![]() 相似?若存在,求t的值;若不存在,請說明理由.
相似?若存在,求t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在同一平面內(nèi),若一個點到一條直線的距離不大于1,則稱這個點是該直線的“伴侶點”.
在平面直角坐標(biāo)系中,已知點M(1,0),過點M作直線l平行于y軸,點A(﹣1,a),點B(b,2a),點 C(﹣![]() ,a﹣1),將三角形ABC進(jìn)行平移,平移后點A的對應(yīng)點為D,點B的對應(yīng)點為E,點C的對應(yīng)點為F.
,a﹣1),將三角形ABC進(jìn)行平移,平移后點A的對應(yīng)點為D,點B的對應(yīng)點為E,點C的對應(yīng)點為F.
(1)試判斷點A是否是直線l的“伴侶點”?請說明理由;
(2)若點F剛好落在直線l上,F的縱坐標(biāo)為a+b,點E落在x軸上,且三角形MFD的面積為![]() ,試判斷點B是否是直線l的“伴侶點”?請說明理由.
,試判斷點B是否是直線l的“伴侶點”?請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“揚州漆器”名揚天下,某網(wǎng)店專門銷售某種品牌的漆器筆筒,成本為30元/件,每天銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間存在一次函數(shù)關(guān)系,如圖所示.
(元)之間存在一次函數(shù)關(guān)系,如圖所示.

(1)求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)如果規(guī)定每天漆器筆筒的銷售量不低于240件,當(dāng)銷售單價為多少元時,每天獲取的利潤最大,最大利潤是多少?
(3)該網(wǎng)店店主熱心公益事業(yè),決定從每天的銷售利潤中捐出150元給希望工程,為了保證捐款后每天剩余利潤不低于3600元,試確定該漆器筆筒銷售單價的范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com