
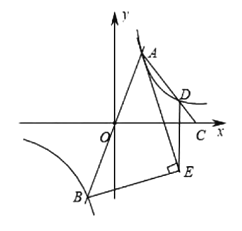
【題目】如圖,過原點的直線與反比例函數![]() 的圖象交于
的圖象交于![]() 兩點,點
兩點,點![]() 在第一象限。點
在第一象限。點![]() 在
在![]() 軸正半軸上,連結
軸正半軸上,連結![]() 交反比例函數圖象于點
交反比例函數圖象于點![]() 。
。![]() 為
為![]() 的平分線,過點
的平分線,過點![]() 作
作![]() 的垂線,垂足為
的垂線,垂足為![]() ,連結
,連結![]() 。若
。若![]() ,
,![]() 的面積為6,則
的面積為6,則![]() 的值為________。
的值為________。
【答案】![]()
【解析】
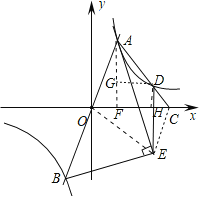
連接OE,CE,過點A作AF⊥x軸,過點D作DH⊥x軸,過點D作DG⊥AF;由AB經過原點,則A與B關于原點對稱,再由BE⊥AE,AE為∠BAC的平分線,可得AD∥OE,進而可得S△ACE=S△AOC;設點A(m,![]() ),由已知條件AC=3DC,DH∥AF,可得3DH=AF,則點D(3m,
),由已知條件AC=3DC,DH∥AF,可得3DH=AF,則點D(3m,![]() ),證明△DHC∽△AGD,得到S△HDC=
),證明△DHC∽△AGD,得到S△HDC=![]() S△ADG,所以S△AOC=S△AOF+S梯形AFHD+S△HDC=
S△ADG,所以S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() k+
k+![]() +
+![]() =9;即可求解;
=9;即可求解;
解:
連接OE,CE,過點A作AF⊥x軸,過點D作DH⊥x軸,過點D作DG⊥AF,
∵過原點的直線與反比例函數y=![]() (k>0)的圖象交于A,B兩點,
(k>0)的圖象交于A,B兩點,
∴A與B關于原點對稱,
∴O是AB的中點,
∵BE⊥AE,
∴OE=OA,
∴∠OAE=∠AEO,
∵AE為∠BAC的平分線,
∴∠DAE=∠AEO,
∴AD∥OE,
∴S△ACE=S△AOC,
∵AC=3DC,△ADE的面積為6,
∴S△ACE=S△AOC=9,
設點A(m,![]() ),
),
∵AC=3DC,DH∥AF,
∴3DH=AF,
∴D(3m,![]() ),
),
∵CH∥GD,AG∥DH,
∴△DHC∽△AGD,
∴S△HDC=![]() S△ADG,
S△ADG,
∵S△AOC=S△AOF+S梯形AFHD+S△HDC=![]() k+
k+![]() ×(DH+AF)×FH+S△HDC=
×(DH+AF)×FH+S△HDC=![]() k+
k+![]() ×
×![]() ×2m+
×2m+
![]() ×
×![]() ×
×![]() ×2m=
×2m=![]() k+
k+![]() +
+![]() =9,
=9,
∴2k=9,
∴k=![]() ;
;
故答案為![]() .
.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:初中數學 來源: 題型:
【題目】兩個一次函數l1、l2的圖象如圖:

(1)分別求出l1、l2兩條直線的函數關系式;
(2)求出兩直線與y軸圍成的△ABP的面積;
(3)觀察圖象:請直接寫出當x滿足什么條件時,l1的圖象在l2的下方.
查看答案和解析>>
科目:初中數學 來源: 題型:
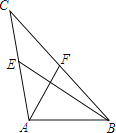
【題目】新定義:我們把兩條中線互相垂直的三角形稱為“中垂三角形”如圖所示,△ABC中AF、BE是中線,且AF⊥BE,垂足為P,像△ABC這樣的三角形稱為“中垂三角形”,如果∠ABE=30°,AB=6,那么此時AC的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在Rt△ABC中,∠C=90°,AC=4,BC=3,O是AB上一點,且AO=2.
(1)求點O到直線AC的距離OH的長;
(2)若P是邊AC上一個動點,作PQ⊥OP交線段BC于Q(不與B、C重合),設AP=x,CQ=y,試求y關于x的函數解析式,并寫出定義域;
(3)在(2)的條件下,當AP為多少時能使△OPQ與△CPQ相似.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣2(a+1)x+a2+3=0有兩個實數根x1,x2
(1)求實數a的取值范圍
(2)若等腰△ABC的三邊長分別為x1,x2,6,求△ABC的周長
(3)是否存在實數a,使x1,x2恰是一個邊長為![]() 的菱形的兩條對角線的長?若存在,求出這個菱形的面積;若不存在,說明理由.
的菱形的兩條對角線的長?若存在,求出這個菱形的面積;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
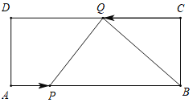
【題目】已知矩形ABCD中,AB=10,BC=4,點P從點A出發,以每秒1個單位長度沿AB方向向B運動,點Q從點C出發,以每秒2個單位長度沿CD方向向D運動,如果P、Q兩點同時出發,問幾秒后以△BPQ是直角三角形?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com