
【題目】經過三角形一邊的中點,畫另一邊的平行線,則這條平行線平分第三邊;三角形兩邊中點之間線段的長度等于第三邊長度的一半.
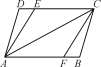
如圖,要判定AB∥CD,需要哪些條件?根據是什么?
【答案】見解析.
【解析】
利用平行線判定定理,內錯角相等,兩直線平行;同旁內角互補,兩直線平行;同位角相等,兩直線平行即可解題.
①若考慮截線AD,則需∠D+∠DAB=180°,根據是同旁內角互補,兩直線平行.
②若考慮截線AE,則需∠CEA+∠EAB=180°,根據是同旁內角互補,兩直線平行或∠DEA=∠EAB,根據是內錯角相等,兩直線平行.
③若考慮截線AC,則需∠DCA=∠CAB,根據是內錯角相等,兩直線平行.
④若考慮截線FC,則需∠DCF+∠AFC=180°,根據是同旁內角互補,兩直線平行或∠DCF=∠BFC,根據是內錯角相等,兩直線平行.
⑤若考慮截線BC,則需∠DCB+∠B=180°,根據是同旁內角互補,兩直線平行.


科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系中的位置如圖所示,先將△ABC向右平移3個單位,再向下平移1個單位到△A1B1C1,△A1B1C1和△A2B2C2關于x軸對稱

(1)畫出△A1B1C1和△A2B2C2
(2)在x軸上確定一點P,使BP+A1P的值最小,直接寫出P的坐標為________
(3)點Q在坐標軸上且滿足△ACQ為等腰三角形,則這樣的Q點有 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網格中,點A、點B均為格點.
(1)AB的長等于;
(2)若點C是以AB為底邊的等腰直角三角形的頂點,點D在邊AC上,且滿足S△ABD= ![]() S△ABC . 請在如圖所示的網格中,用無刻度的直尺,畫出線段BD,并簡要說明點D的位置時如何找到的(不要求證明). .
S△ABC . 請在如圖所示的網格中,用無刻度的直尺,畫出線段BD,并簡要說明點D的位置時如何找到的(不要求證明). .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是小華做觀察水的沸騰實驗時所記錄的數據:

(1)時間是8分鐘時,水的溫度為_____;
(2)此表反映了變量_____和_____之間的關系,其中_____是自變量,_____是因變量;
(3)在_____時間內,溫度隨時間增加而增加;_____時間內,水的溫度不再變化.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩臺機床同時生產同一種零件,在10天中兩臺機床每天生產的次品數如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分別計算兩組數據的平均數和方差;
(2)從結果看,在10天中哪臺機床出現次品的波動較小?
(3)由此推測哪臺機床的性能較好
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象分別與反比例函數y= ![]() 的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB.
的圖象在第一象限交于點A(4,3),與y軸的負半軸交于點B,且OA=OB. 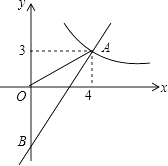
(1)求函數y=kx+b和y= ![]() 的表達式;
的表達式;
(2)已知點C(0,5),試在該一次函數圖象上確定一點M,使得MB=MC,求此時點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(7分)某學校舉行演講比賽,選出了10名同學擔任評委,并事先擬定從如下4個方案中選擇合理的方案來確定每個演講者的最后得分(滿分為10分):
方案1:所有評委所給分的平均數,
方案2:在所有評委所給分中,去掉一個最高分和一個最低分.然后再計算其余給分的l平均數.
方案3:所有評委所給分的中位效.
方案4:所有評委所給分的眾數.
為了探究上述方案的合理性.先對某個同學的演講成績進行了統計實驗.下面是這個同學的得分統計圖:

(1)分別按上述4個方案計算這個同學演講的最后得分;
(2)根據(1)中的結果,請用統計的知識說明哪些方案不適臺作為這個同學演講的最后得分,并給出該同學的最后得分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家生產并銷售某種產品,假設銷售量與產量相等,如圖中的折線ABD,線段CD分別表示該產品每千克生產成本y1(單位:元),銷售價y2(單位:元)與產量x(單位:kg)之間的函數關系.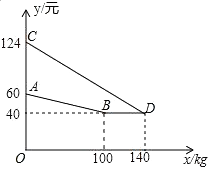
(1)請解釋圖中點D的實際意義.
(2)求線段CD所表示的y2與x之間的函數表達式.
(3)當該產品產量為多少時,獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com