
【題目】某廠家生產并銷售某種產品,假設銷售量與產量相等,如圖中的折線ABD,線段CD分別表示該產品每千克生產成本y1(單位:元),銷售價y2(單位:元)與產量x(單位:kg)之間的函數關系.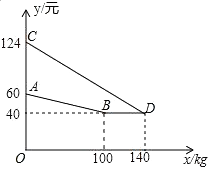
(1)請解釋圖中點D的實際意義.
(2)求線段CD所表示的y2與x之間的函數表達式.
(3)當該產品產量為多少時,獲得的利潤最大?最大利潤是多少?
【答案】
(1)解:點D的實際意義:當產量為140kg時,該產品每千克生產成本與銷售價相等,都為40元
(2)解:設線段CD所表示的y2與x之間的函數表達式為y2=k1x+b1,
∵點(0,124),(140,40)在函數y2=k1x+b1的圖象上
∴ ![]() ,解得:
,解得:  ,
,
∴y2與x之間的函數表達式為y2=﹣ ![]() x+124(0≤x≤140)
x+124(0≤x≤140)
(3)解:設線段AB所表示的y1與x之間的函數表達式為y1=k2x+b2,
∵點(0,60),(100,40)在函數y1=k2x+b2的圖象上
∴ ![]() ,解得:
,解得:  ,
,
∴y1與x之間的函數表達式為y1=﹣ ![]() x+60(0≤x≤100)
x+60(0≤x≤100)
設產量為x千克時,獲得的利潤為W元
①當0≤x≤100時,W=[(﹣ ![]() x+124)﹣(﹣
x+124)﹣(﹣ ![]() x+60)]x=﹣
x+60)]x=﹣ ![]() (x﹣80)2+2560,
(x﹣80)2+2560,
∴當x=80時,W的值最大,最大值為2560元.
②當100≤x≤140時,W=[(﹣ ![]() x+124)﹣40]x=﹣
x+124)﹣40]x=﹣ ![]() (x﹣70)2+2940
(x﹣70)2+2940
由﹣ ![]() <0知,當x≥70時,W隨x的增大而減小
<0知,當x≥70時,W隨x的增大而減小
∴當x=100時,W的值最大,最大值為2400元.
∵2560>2400,
∴當該產品的質量為80kg時,獲得的利潤最大,最大利潤為2560元
【解析】(1)交點D為x取相同數時y1=y2所以易得點D的實際意義。
(2)已知點C,點D坐標,所以易由待定系數法求得直線CD的解析式。
(3)由于銷售量與產量的函數圖像分為兩段,所以需要分情況討論,而我們的利潤是(售價-成本)×數量,所以結合(2)中的解析式可得利潤的解析式分別為①當0≤x≤100時W==﹣ ![]() (x﹣80)2+2560②當100≤x≤140時,W=﹣
(x﹣80)2+2560②當100≤x≤140時,W=﹣ ![]() (x﹣70)2+2940,結合兩個函數的最值,可得結果。
(x﹣70)2+2940,結合兩個函數的最值,可得結果。
【考點精析】關于本題考查的二次函數的性質和二次函數的最值,需要了解增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小;如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a才能得出正確答案.


科目:初中數學 來源: 題型:
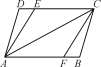
【題目】經過三角形一邊的中點,畫另一邊的平行線,則這條平行線平分第三邊;三角形兩邊中點之間線段的長度等于第三邊長度的一半.
如圖,要判定AB∥CD,需要哪些條件?根據是什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】乘法公式的探究及應用.
(1)如圖1,可以求出陰影部分的面積是 (寫成兩數平方差的形式);
(2)如圖2,若將陰影部分裁剪下來,重新拼成一個矩形,它的寬是 ,長是 ,面積是 (寫成多項式乘法的形式);
(3)比較圖1、圖2兩圖的陰影部分面積,可以得到乘法公式 (用式子表達);
(4)運用你所得到的公式,計算下列各題:
①(2m+n-p)(2m-n+p);②10.3×9.7.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛汽車行駛時的耗油量為![]() 升/千米,如圖是油箱剩余油量
升/千米,如圖是油箱剩余油量![]() (升)關于加滿油后行駛的路程
(升)關于加滿油后行駛的路程![]() (千米)的函數圖象.
(千米)的函數圖象.
(1)根據圖象,直接寫出汽車行駛![]() 千米時,油箱內的剩余油量為 升,加滿油時油箱的油量為 升;
千米時,油箱內的剩余油量為 升,加滿油時油箱的油量為 升;
(2)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)計算該汽車在剩余油量![]() 升時,已行駛的路程.
升時,已行駛的路程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】基本圖形:在Rt△![]() 中,
中,![]() ,
,![]() 為
為![]() 邊上一點(不與點
邊上一點(不與點![]() ,
,![]() 重合),將線段
重合),將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() .
.
探索:(1)連接![]() ,如圖①,試探索線段
,如圖①,試探索線段![]() 之間滿足的等量關系,并證明結論;
之間滿足的等量關系,并證明結論;
(2)連接![]() ,如圖②,試探索線段
,如圖②,試探索線段![]() 之間滿足的等量關系,并證明結論;
之間滿足的等量關系,并證明結論;

聯想:(3)如圖③,在四邊形![]() 中,
中,![]() .若
.若![]() ,
,![]() ,則
,則![]() 的長為 .
的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數圖象的對稱軸為直線x=2,頂點為點C,直線y=x+m與該二次函數的圖象交于點A,B兩點,其中點A的坐標為(5,8),點B在y軸上.
(1)求m的值和該二次函數的表達式.P為線段AB上一個動點(點P不與A,B兩點重合),過點P作x軸的垂線,與這個二次函數的圖象交于點E.
①設線段PE的長為h,求h與x之間的函數關系式,并寫出自變量x的取值范圍.
②若直線AB與這個二次函數圖象的對稱軸的交點為D,求當四邊形DCEP是平行四邊形時點P的坐標.
(2)若點P(x,y)為直線AB上的一個動點,試探究:以PB為直徑的圓能否與坐標軸相切?如果能請求出點P的坐標,如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為慶祝“六一”兒童節,某市中小學統一組織文藝匯演,甲、乙兩所學校共92人(其中甲校的人數多于乙校的人數,且甲校的人數不足90人)準備統一購買服裝參加演出;下面是某服裝廠給出的演出服裝的價格表
購買服裝的套數 | 1套至45套 | 46套至90套 | 91套以上 |
每套服裝的價格 | 60元 | 50元 | 40元 |
(1)如果兩所學校分別單獨購買服裝一共應付5000元,甲、乙兩所學校各有多少學生準備參加演出?
(2)如果甲校有10名同學抽調去參加書法繪畫比賽不能參加演出,請你為兩所學校設計一種最省錢的購買服裝方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面說法正確的是個數有( )
①如果三角形三個內角的比是1:2:3,那么這個三角形是直角三角形;
②如果三角形的一個外角等于與它相鄰的一個內角,則這么三角形是直角三角形;
③如果一個三角形的三條高的交點恰好是三角形的一個頂點,那么這個三角形是直角三角形;
④如果∠A=∠B=![]() ∠C,那么△ABC是直角三角形;
∠C,那么△ABC是直角三角形;
⑤若三角形的一個內角等于另兩個內角之差,那么這個三角形是直角三角形;
⑥在△ABC中,若∠A+∠B=∠C,則此三角形是直角三角形.
A.3個 B.4個 C.5個 D.6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解七年級男生體質健康情況,隨機抽取若干名男生進行測試,測試結果分為優秀、良好、合格、不合格四個等級,統計整理數據并繪制圖1、圖2兩幅不完整的統計圖,請根據圖中信息回答下列問題: 
(1)本次接收隨機抽樣調查的男生人數為人,扇形統計圖中“良好”所對應的圓心角的度數為;
(2)補全條形統計圖中“優秀”的空缺部分;
(3)若該校七年級共有男生480人,請估計全年級男生體質健康狀況達到“良好”的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com