
【題目】如圖,在每個小正方形的邊長為1的網格中,點A、點B均為格點.
(1)AB的長等于;
(2)若點C是以AB為底邊的等腰直角三角形的頂點,點D在邊AC上,且滿足S△ABD= ![]() S△ABC . 請在如圖所示的網格中,用無刻度的直尺,畫出線段BD,并簡要說明點D的位置時如何找到的(不要求證明). .
S△ABC . 請在如圖所示的網格中,用無刻度的直尺,畫出線段BD,并簡要說明點D的位置時如何找到的(不要求證明). .
【答案】
(1)![]()
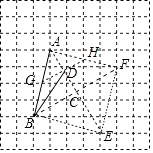
(2)以AB為邊連接格點,構成正方形ABEF,連接對角線AE、BF,則對角線交點即為C點,正方形相鄰兩邊分別與網格線有兩個交點G、H,且為兩邊中點,連接GH與AE交于D點,連接BD,BD即為所求
【解析】解:(1)AB= ![]() =
= ![]() ;
;
所以答案是 ![]() (2)如圖,以AB為邊連接格點,構成正方形ABEF,連接對角線AE、BF,則對角線交點即為C點,正方形相鄰兩邊分別與網格線有兩個交點G、H,且為兩邊中點,連接GH與AE交于D點,連接BD,BD即為所求.
(2)如圖,以AB為邊連接格點,構成正方形ABEF,連接對角線AE、BF,則對角線交點即為C點,正方形相鄰兩邊分別與網格線有兩個交點G、H,且為兩邊中點,連接GH與AE交于D點,連接BD,BD即為所求.
所以答案是:以AB為邊連接格點,構成正方形ABEF,連接對角線AE、BF,則對角線交點即為C點,正方形相鄰兩邊分別與網格線有兩個交點G、H,且為兩邊中點,連接GH與AE交于D點,連接BD,BD即為所求.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】已知數軸上三點![]() 、
、![]() 、
、![]() 表示的數分別為4、0、
表示的數分別為4、0、![]() ,動點
,動點![]() 從
從![]() 點出發,以每秒3個單位的速度沿數軸向左勻速運動.
點出發,以每秒3個單位的速度沿數軸向左勻速運動.
(1)當點![]() 到點
到點![]() 的距離與點
的距離與點![]() 到點
到點![]() 的距離相等時,點
的距離相等時,點![]() 在數軸上表示的數是 .
在數軸上表示的數是 .
(2)另一動點![]() 從點
從點![]() 出發,以每秒2個單位的速度沿數軸向左勻速運動,若點
出發,以每秒2個單位的速度沿數軸向左勻速運動,若點![]() 、
、![]() 同時出發,問點
同時出發,問點![]() 運動多長時間追上點
運動多長時間追上點![]() ?
?
(3)若點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 的中點,點
的中點,點![]() 在運動過程中,線段
在運動過程中,線段![]() 的長度是否發生變化?若發生變化,請你說明理由;若不變,請你畫出圖形,并求出線段
的長度是否發生變化?若發生變化,請你說明理由;若不變,請你畫出圖形,并求出線段![]() 的長度.
的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車專賣店銷售A,B兩種型號的新能源汽車.上周售出1輛A型車和3輛B型車,銷售額為96萬元;本周已售2輛A型車和1輛B型車,銷售額為62萬元.
(1)求每輛A型車和B型車的售價各多少萬元.
(2)甲公司擬向該店購買A,B兩種型號的新能源汽車共6輛,購車費不少于130萬元,且不超過140萬元. 則有哪幾種購車方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知動點![]() 以每秒
以每秒![]() 的速度沿如圖甲所示的邊框按從
的速度沿如圖甲所示的邊框按從![]() 的路徑移動,其中
的路徑移動,其中![]() ,相應的
,相應的![]() 的面積
的面積![]() 關于時間
關于時間![]() 的函數圖象如圖乙所示,若
的函數圖象如圖乙所示,若![]() ,試回答下列問題:
,試回答下列問題:


(1)如圖甲![]() _______
_______![]() ;
;![]() ________
________![]() .
.
(2)如圖乙,圖中的![]() ________,
________,![]() _______.
_______.
(3)在上述運動過程中,![]() 面積的最大值是________
面積的最大值是________![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,我們把杜甫(絕句)整齊排列放在平面直角坐標系中:

(1)“東”、“窗”和“柳”的坐標依次是:______、______和________.;
(2)將第1行與第3行對調,再將第4列與第6列對調,“里”由開始的坐標________依次變換到:________和________;
(3)“門”開始的坐標是(1,1),使它的坐標到(3,2),應該哪兩行對調,同時哪兩列對調?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖①由4根火柴棍圍成;圖②由12根火柴棍圍成;圖③由24根火柴棍圍成;…按此規律,則第⑥個圖形由( )根火柴棍圍成.
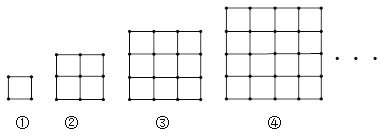
A. 60 B. 72 C. 84 D. 112
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果兩個三角形的兩條邊對應相等,夾角互補,那么這兩個三角形叫做互補三角形,如圖2,分別以△ABC的邊AB、AC為邊向外作正方形ABDE和ACGF,則圖中的兩個三角形就是互補三角形.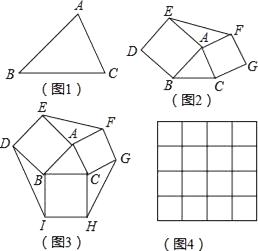
(1)用尺規將圖1中的△ABC分割成兩個互補三角形;
(2)證明圖2中的△ABC與△AEF兩個互補三角形面積相等;
(3)如圖3,在圖2的基礎上再以BC為邊向外作正方形BCHI.
①已知三個正方形面積分別是17、13、10,在如圖4的網格中(網格中每個小正方形的邊長為1)畫出邊長為 ![]() 、
、 ![]() 、
、 ![]() 的三角形,并計算圖3中六邊形DEFGHI的面積.
的三角形,并計算圖3中六邊形DEFGHI的面積.
②若△ABC的面積為2,求以EF、DI、HG的長為邊的三角形面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經過三角形一邊的中點,畫另一邊的平行線,則這條平行線平分第三邊;三角形兩邊中點之間線段的長度等于第三邊長度的一半.
如圖,要判定AB∥CD,需要哪些條件?根據是什么?
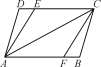
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】乘法公式的探究及應用.
(1)如圖1,可以求出陰影部分的面積是 (寫成兩數平方差的形式);
(2)如圖2,若將陰影部分裁剪下來,重新拼成一個矩形,它的寬是 ,長是 ,面積是 (寫成多項式乘法的形式);
(3)比較圖1、圖2兩圖的陰影部分面積,可以得到乘法公式 (用式子表達);
(4)運用你所得到的公式,計算下列各題:
①(2m+n-p)(2m-n+p);②10.3×9.7.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com