
【題目】如圖1,將兩個完全相同的三角形紙片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作發現:如圖2,固定△ABC,使△DEC繞點C順時針旋轉.當點D恰好落在AB邊上時,填空:
①線段DE與AC的位置關系是 ;
②設△BDC的面積為S1,△AEC的面積為S2,則S1與S2的數量關系是 ;
(2)猜想論證:
當△DEC繞點C旋轉到圖3所示的位置時,小明猜想(1)中S1與S2的數量關系仍然成立,并嘗試分別作出了△BDC和△AEC中BC,CE邊上的高,請你證明小明的猜想.
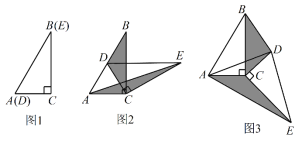
【答案】(1)DE∥AC;S1=S2;(2)證明見解析.
【解析】
試題(1)①根據旋轉的性質可得AC=CD,然后求出△ACD是等邊三角形,根據等邊三角形的性質可得∠ACD=60,然后根據內錯角相等,兩直線平行解答;
②根據等邊三角形的性質可得AC=AD,再根據直角三角形30角所對的直角邊等于斜邊的一半求出AC=![]() AB,然后求出AC=BE,再根據等邊三角形的性質求出點C到AB的距離等于點D到AC的距離,然后根據等底等高的三角形的面積相等解答;
AB,然后求出AC=BE,再根據等邊三角形的性質求出點C到AB的距離等于點D到AC的距離,然后根據等底等高的三角形的面積相等解答;
(2)根據旋轉的性質可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用"角角邊"證明△ACN和△DCM全等,根據全等三角形對應邊相等可得AN=DM,然后利用等底等高的三角形的面積相等證明;
試題解析:
(1)①線段DE與AC的位置關系是 平行 .②S1與S2的數量關系是 相等 .
證明:如圖2,過D作DN⊥AC交AC于點N,過E作EM⊥AC交AC延長線于M,過C作CF⊥AB交AB于點F.
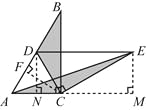
由①可知△ADC是等邊三角形,DE∥AC,
∴DN=CF,DN=EM.
∴CF=EM.
∵∠ACB=90,∠B=30,
∴AB=2AC.
又∵AD=AC,
∴BD=AC.
∵S1=![]() CF·BD,S2=
CF·BD,S2=![]() AC·EM,
AC·EM,
∴S1=S2.
證明:如圖3,作DG⊥BC于點G,AH⊥CE交EC延長線于點H.

∵∠DCE=∠ACB=90∴∠DCG+∠ACE=180.
又∵∠ACH+∠ACE=180,∴∠ACH=∠DCG.
又∵∠CHA=∠CGD=90,AC=CD,
∴△AHC≌△DGC.
∴AH=DG.
又∵CE=CB,
∴S1=S2.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數學 來源: 題型:
【題目】長方形紙片![]() 中,
中,![]() ,
,![]() ,把這張長方形紙片
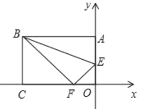
,把這張長方形紙片![]() 如圖放置在平面直角坐標系中,在邊
如圖放置在平面直角坐標系中,在邊![]() 上取一點
上取一點![]() ,將
,將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 恰好落在
恰好落在![]() 邊上的點
邊上的點![]() 處.
處.
(1)點![]() 的坐標是____________________;點
的坐標是____________________;點![]() 的坐標是__________________________;
的坐標是__________________________;
(2)在![]() 上找一點
上找一點![]() ,使
,使![]() 最小,求點
最小,求點![]() 的坐標;
的坐標;
(3)在(2)的條件下,點![]() 是直線
是直線![]() 上一個動點,設
上一個動點,設![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數 關系式.
的函數 關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
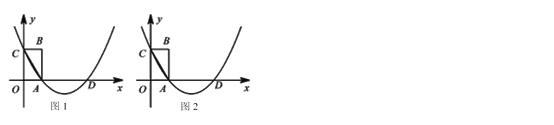
【題目】如圖,在平面直角坐標系中,矩形OABC的邊OA,OC分別位于x軸,y軸上,經過A,C兩點的拋物線變x軸于另一點D,連接AC.請你只用無刻度的直尺按要求畫圖.
(1)在圖1中的拋物線上,畫出點E,使DE=AC;
(2)在圖2中的拋物線上,畫出拋物線的頂點F.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電信公司手機的通訊卡有![]() ,
,![]() 兩種業務類型:
兩種業務類型:![]() 類卡收費標準是:不管通話時間多長,每部手機每月必須繳月租費12元,另外,通話費按0.2元/分鐘計;
類卡收費標準是:不管通話時間多長,每部手機每月必須繳月租費12元,另外,通話費按0.2元/分鐘計;![]() 類卡收費標準是:沒有月租,但通話費按0.25元/分鐘計.如圖所示,是每月應繳費用
類卡收費標準是:沒有月租,但通話費按0.25元/分鐘計.如圖所示,是每月應繳費用![]() (元)與通話時間
(元)與通話時間![]() (分鐘)之間的函數圖象.下列結論:
(分鐘)之間的函數圖象.下列結論:
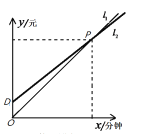
①圖中![]() 是
是![]() 類卡的收費方式所表示的函數圖象;
類卡的收費方式所表示的函數圖象;
②若李海本月的通話時間為180分鐘,則他選擇![]() 類卡省錢;
類卡省錢;
③若本月李海預繳了100元的話費,則他選擇![]() 類卡劃算;
類卡劃算;
④若![]() 類卡比
類卡比![]() 類卡的話費多10元,則
類卡的話費多10元,則![]() 類卡和
類卡和![]() 類卡的通話時間都是40分鐘或
類卡的通話時間都是40分鐘或![]() 類卡比
類卡比![]() 類卡的通話時間多40分鐘且
類卡的通話時間多40分鐘且![]() 類卡和
類卡和![]() 類卡的通話時間分別為240分鐘和200分鐘.其中正確的結論有( )
類卡的通話時間分別為240分鐘和200分鐘.其中正確的結論有( )
A.①②③④B.②③④C.②③D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,是擺放在張明和趙華面前的甲和乙兩個圓柱形水槽從正面看到的圖形,甲槽中有適量的水,乙槽中有一圓柱形鐵塊(圓柱形鐵塊的下底面完全落在水槽底面,鐵塊的高度低于水槽的高度).張明將甲槽中的水勻速注入乙槽,同時趙華計時并測量,最后他們把甲、乙兩個水槽中水的深度![]() 與注水時間
與注水時間![]() 之間的關系畫出了如圖所示的函數圖象.請根據函數圖象提供的信息,解答下列問題:
之間的關系畫出了如圖所示的函數圖象.請根據函數圖象提供的信息,解答下列問題:
(1)如圖所示,線段![]() 表示 槽中水的深度與注水時間之間的關系;折線
表示 槽中水的深度與注水時間之間的關系;折線![]() 表示 槽中水的深度與注水時間之間的關系(以上兩空填“甲” 或“乙”);點
表示 槽中水的深度與注水時間之間的關系(以上兩空填“甲” 或“乙”);點![]() 的縱坐標14表示的實際意義是 ;
的縱坐標14表示的實際意義是 ;
(2)分別求線段![]() 、線段
、線段![]() 的函數表達式;
的函數表達式;
(3)注水多長時間時,甲、乙兩個水槽中水的深度相同?
(4)若乙水槽的底面積為![]() (水槽壁的厚度不計),求乙水槽中鐵塊的體積是多少
(水槽壁的厚度不計),求乙水槽中鐵塊的體積是多少![]() ?
?


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的袋中裝有5個只有顏色不同的球,其中3個黃球,2個黑球.
(1)求從袋中同時摸出的兩個球都是黃球的概率;
(2)現將黑球和白球若干個(黑球個數是白球個數的2倍)放入袋中,攪勻后,若從袋中摸出一個球是黑球的概率是![]() ,求放入袋中的黑球的個數.
,求放入袋中的黑球的個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,BC為⊙O的切線,D為⊙O上的一點,CD=CB,延長CD交BA的延長線于點E.
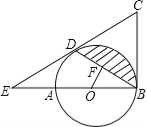
(1)求證:CD為⊙O的切線;
(2)若BD的弦心距OF=1,∠ABD=30°,求圖中陰影部分的面積.(結果保留π)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com