【題目】將連續的偶數2，4，6，8，…，如圖所示排列：
(1)求圖中十字框內5個數的和與中間的數16的倍數關系.
(2)若將十字框上下左右移動，可框住另外的五個數，請說明這五個數的和與十字框最中間的數之間存在的關系.
(3)若將十字框上下左右移動，框住的五個數的和能等于2019嗎？若能，請寫出這五個數；若不能，請說明理由.
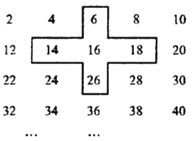
【答案】(1)五個數的和為16的5倍；(2)五個數的和是十字框最中間的數的5倍.；(3)不能.
【解析】
（1）將十字框內5個數的和除以16即可得到答案；
（2）設十字框中間的數為
，則它上面的數為
，下面的數為
，左面的數為
，右面的數為
，求出這五個數之和，即可得出答案.
（3）根據（2）得出的結論可知，十字框中五數之和一定是5的倍數，而2019不是5的倍數，可得答案.
解：(1)
，
，
所以十字框中五個數的和為16的5倍.
(2)設中間的數為，則它上面的數為，下面的數為，左面的數為，右面的數為.
所以
所以五個數的和是十字框最中間的數的5倍.
(3)不能.
十字框中五數之和一定是5的倍數，而2019不是5的倍數，所以十字框中的五數之和不能等于2019.
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=
x2+mx+n與x軸相交于點A、B兩點，過點B的直線y=x+b交拋物線于另一點C（－5,6），點D是線段BC上的一個動點（點D與點B、C不重合），作DE∥AC，交該拋物線于點E，
（1）求m,n,b的值；
（2）求tan∠ACB；
（3）探究在點D運動過程中，是否存在∠DEA=45°，若存在，則求此時線段AE的長；若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
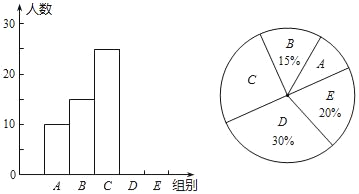
【題目】我校舉行“漢字聽寫”比賽，每位學生聽寫漢字39個，比賽結束后隨機抽查部分學生的聽寫結果，以下是根據抽查結果繪制的統計圖的一部分．
組別 | 正確數字x | 人數 |
A | 0≤x＜8 | 10 |
B | 8≤x＜16 | 15 |
C | 16≤x＜24 | 25 |
D | 24≤x＜32 | m |
E | 32≤x＜40 | n |
根據以上信息解決下列問題：
（1）在統計表中，m= ，n= ，并補全條形統計圖．
（2）扇形統計圖中“C組”所對應的圓心角的度數是 ．
（3）有三位評委老師，每位老師在E組學生完成學校比賽后，出示“通過”或“淘汰”或“待定”的評定結果．學校規定：每位學生至少獲得兩位評委老師的“通過”才能代表學校參加鄂州市“漢字聽寫”比賽，請用樹形圖求出E組學生王云參加鄂州市“漢字聽寫”比賽的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知OE是∠AOC的角平分線，OD是∠BOC的角平分線．
（1）若∠AOC=120°，∠BOC=30°，求∠DOE的度數；
（2）若∠AOB=90°，∠BOC=α，求∠DOE的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分別是∠BAC、∠BCA的平分線,AD、CE相交于點F.
(1)請你判斷并寫出FE與FD之間的數量關系(不需證明);
(2)如圖②,如果∠ACB不是直角,其他條件不變,那么在(1)中所得的結論是否仍然成立?若成立,請證明;若不成立,請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是 ( )
A.凌晨氣溫為-5℃，中午氣溫比凌晨上升5℃，所以中午的氣溫為+5℃
B.-(-2)3 和 -23互為相反數
C.-5πxy3 的系數是-5，次數是4
D.-︱-6
︱=-(-6)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知數軸上點A表示的數為6，B是數軸上一點，且AB=10，動點P從點A出發，以每秒6個單位長度的速度沿數軸向左勻速運動，設運動時間為t（t＞0）秒，
（1）寫出數軸上點B所表示的數 ；
（2）點P所表示的數 ；（用含t的代數式表示）；
（3）M是AP的中點，N為PB的中點，點P在運動的過程中，線段MN的長度是否發生變化？若變化，說明理由；若不變，請你畫出圖形，并求出線段MN的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列兩個等式：
，
，給出定義如下：我們稱使等式a﹣b＝ab+1的成立的一對有理數a，b為“共生有理數對”，記為（a，b），如：數對
，
，都是“共生有理數對”．
（1）數對
，
中是“共生有理數對”的是 ；
（2）若（m，n）是“共生有理數對”，則（﹣n，﹣m） “共生有理數對”（填“是”或“不是”）；
（3）請再寫出一對符合條件的“共生有理數對”為 ；（注意：不能與題目中已有的“共生有理數對”重復）
（4）若（a，3）是“共生有理數對”，求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】探索代數式
與代數式
的關系.
（1）當
，
時，分別計算兩個代數式的值.
（2）當
，
時，分別計算兩個代數式的值.
（3）你發現了什么規律?
（4）利用你發現的規律計算:20182-2×2018×2019+20192.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com