【題目】某校7名學生在某次測量體溫（單位：℃）時得到如下數據：36.3，36.4，36.5，36.7，36.6，36.5，36.5，對這組數據描述正確的是（ ）
A.眾數是36.5B.中位數是36.7
C.平均數是36.6D.方差是0.4
科目：初中數學 來源： 題型：
【題目】某校為了解本校初中學生在學校號召的“積極公益”活動中周末參加公益的時間（單位：h），隨機調查了該校的部分初中學生.根據調查結果，繪制出如下的統計圖①和圖②.請根據相關信息，解答下列問題：
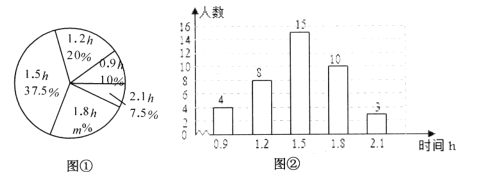
（1）本次接受調查的初中學生人數為________，圖①中m的值為________；
（2）求統計的這部分學生參加公益的時間數據的平均數、眾數和中位數；
（3）根據統計的這部分學生周末參加公益時間的樣本數據，若該校共有650名初中學生，估計該校在這個周末參加公益時間大于1h的學生人數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，AE是∠BAC的平分線，∠ABC的平分線BM交AE于點M，點O在AB上，以點O為圓心，OB的長為半徑的圓經過點M，交BC于點G，交AB于點F．
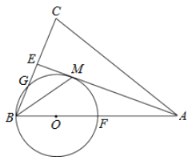
（1）求證：AE為⊙O的切線．
（2）當BC=8，AC=12時，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某經銷商3月份用18000元購進一批T恤衫售完后，4月份用39000元購進單批相同的T恤衫，數量是3月份的2倍，但每件進價漲了10元．
（1）4月份進了這批T恤衫多少件？
（2）4月份，經銷商將這批T恤衫平均分給甲、乙兩家分店銷售，每件標價180元．甲店按標價賣出a件以后，剩余的按標價八折全部售出；乙店同樣按標價賣出a件，然后將b件按標價九折售出，再將剩余的按標價七折全部售出，結果利潤與甲店相同．
①用含a的代數式表示b；
②已知乙店按標價售出的數量不超過九折售出的數量，請你求出乙店利潤的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xoy中，直線
與
軸，
軸分別交于點A和點B.拋物線
經過A,B兩點，且對稱軸為直線
，拋物線與軸的另一交點為點C.
（1）求拋物線的函數表達式；
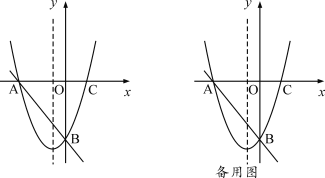
（2）設點E是拋物線上一動點，且點E在直線AB下方.當△ABE的面積最大時，求點E的坐標，及△ABE面積的最大值S；
拋物線上是否還存在其它點M,使△ABM的面積等于中的最大值S,若存在，求出滿足條件的點M的坐標；若不存在，說明理由；
（3）若點F為線段OB上一動點，直接寫出
的最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，對折矩形紙片ABCD使AD與BC重合，得到折痕MN，再把紙片展平．E是AD上一點，將△ABE沿BE折疊，使點A的對應點A′落在MN上．若CD＝5，則BE的長是_____．
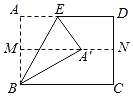
查看答案和解析>>
科目：初中數學 來源： 題型：
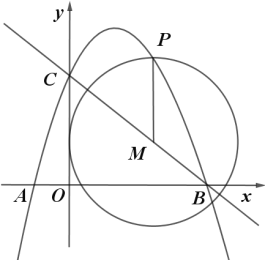
【題目】如圖，拋物線y＝ax2+
x+c經過點A（﹣1，0）和點C （0，3）與x軸的另一交點為點B，點M是直線BC上一動點，過點M作MP∥y軸，交拋物線于點P．
（1）求該拋物線的解析式；
（2）在拋物線上是否存在一點Q，使得△QCO是等邊三角形？若存在，求出點Q的坐標；若不存在，請說明理由；
（3）以M為圓心，MP為半徑作⊙M，當⊙M與坐標軸相切時，求出⊙M的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
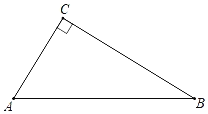
【題目】如圖，在△ABC中，∠C＝90°．
（1）用尺規作∠A的平分線交BC邊于點D（不寫作法，保留作圖痕跡）；
（2）在（1）的基礎上，已知∠B＝30°，AC＝6，則線段AD的長是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】茶葉是安徽省主要經濟作物之一，2020年新茶上市期間，某茶廠為獲得最大利益，根據市場行情，把新茶價格定為400元/kg，并根據歷年的相關數據整理出第x天（1≤x≤15，且x為整數）制茶成本（含采摘和加工）和制茶量的相關信息如下表．假定該茶廠每天制作和銷售的新茶沒有損失，且能在當天全部售出（當天收入=日銷售額-日制茶成本）
制茶成本（元/kg） | 150+10x |
制茶量（kg） | 40+4x |
（1）求出該茶廠第10天的收入；
（2）設該茶廠第x天的收入為y（元）．試求出y與x之間的函數關系式，并求出y的最大值及此時x的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
