
【題目】(1)問題發現
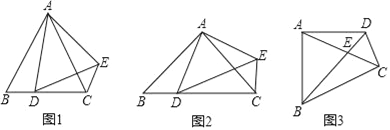
如圖1,△ABC和△ADE均為等邊三角形,點D在邊BC上,連接CE.請填空:
①∠ACE的度數為 ;
②線段AC、CD、CE之間的數量關系為 .
(2)拓展探究
如圖2,△ABC和△ADE均為等腰直角三角形,∠BAC=∠DAE=90°,點D在邊BC上,連接CE.請判斷∠ACE的度數及線段AC、CD、CE之間的數量關系,并說明理由.
(3)解決問題
如圖3,在四邊形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC與BD交于點E,請直接寫出線段AC的長度.
【答案】(1)①60°;②AC=CD+CE;(2)∠ACE=45°,![]() AC=CD+CE(3)
AC=CD+CE(3)![]()
【解析】試題分析:(1)、根據等邊三角形的性質得出∠BAD=∠CAE,從而得出△BAD和△CAE全等,從而得出∠ACE=∠B=60°,根據全等得出BD=CE,從而得出AC=CD+CE;(2)、根據第一題同樣的方法得出△BAD和△CAE全等,從而得出BC=CD+CE,然后根據等腰直角三角形的性質得出BC=![]() AC,從而得出答案;(3)、過A作AC的垂線,交CB的延長線于點F,根據題意得出A、B、C、D四點共圓,即∠ADB=∠ACB=45°,根據第二步的結論AC=
AC,從而得出答案;(3)、過A作AC的垂線,交CB的延長線于點F,根據題意得出A、B、C、D四點共圓,即∠ADB=∠ACB=45°,根據第二步的結論AC=![]() 得出答案.
得出答案.
試題解析:(1)①∵△ABC和△ADE均為等邊三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC, 即∠BAD=∠CAE, ∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,
②線段AC、CD、CE之間的數量關系為:AC=CD+CE;
理由是:由①得:△BAD≌△CAE, ∴BD=CE, ∵AC=BC=BD+CD, ∴AC=CD+CE;
(2)∠ACE=45°,![]() AC=CD+CE,理由是:
AC=CD+CE,理由是:
如圖2,∵△ABC和△ADE均為等腰直角三角形,且∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC, 即∠BAD=∠CAE, ∴△ABD≌△ACE,
∴BD=CE,∠ACE=∠B=45°, ∵BC=CD+BD, ∴BC=CD+CE,
∵在等腰直角三角形ABC中,BC=![]() AC, ∴
AC, ∴![]() AC=CD+CE;
AC=CD+CE;
(3)如圖3,過A作AC的垂線,交CB的延長線于點F,
∵∠BAD=∠BCD=90°,AB=AD=2,CD=1, ∴BD=2![]() ,BC=
,BC=![]() , ∵∠BAD=∠BCD=90°,
, ∵∠BAD=∠BCD=90°,
∴∠BAD+∠BCD=180°, ∴A、B、C、D四點共圓, ∴∠ADB=∠ACB=45°,
∴△ACF是等腰直角三角形, 由(2)得:![]() AC=BC+CD, ∴AC=
AC=BC+CD, ∴AC=![]() =
=![]() =
=![]() .
.



科目:初中數學 來源: 題型:
【題目】(本題滿分10分)如圖,某大樓的頂部豎有一塊廣告牌CD,小明在山坡的坡腳A處測得廣告牌底部D的仰角為60°.沿坡面AB向上走到B處測得廣告牌頂部C的仰角為45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.(測角器的高度忽略不計,結果精確到0.1米.參考數據:
,AB=10米,AE=15米.(測角器的高度忽略不計,結果精確到0.1米.參考數據: ![]() ,
, ![]() )
)
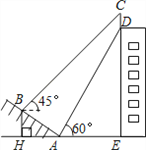
(1)求點B距水平面AE的高度BH;
(2)求廣告牌CD的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
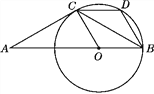
【題目】如圖,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一點O,使OB=OC,以點O為圓心,OB為半徑作圓,過點C作CD∥AB交⊙O于點D,連接BD.
(1)猜想AC與⊙O的位置關系,并證明你的猜想;
(2)試判斷四邊形BOCD的形狀,并證明你的判斷;
(3)已知AC=6,求扇形OBC所圍成的圓錐的底面圓的半徑r.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為滿足市場需求,某超市在五月初五“端午節”來臨前夕,購進一種品牌粽子,每盒進價是40元.超市規定每盒售價不得少于45元.根據以往銷售經驗發現;當售價定為每盒45元時,每天可以賣出700盒,每盒售價每提高1元,每天要少賣出20盒.
(1)試求出每天的銷售量y(盒)與每盒售價x(元)之間的函數關系式;
(2)當每盒售價定為多少元時,每天銷售的利潤P(元)最大?最大利潤是多少?
(3)為穩定物價,有關管理部門限定:這種粽子的每盒售價不得高于58元.如果超市想要每天獲得不低于6000元的利潤,那么超市每天至少銷售粽子多少盒?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)解不等式:![]() .
.
(2)解下列不等式組,并把解集在數軸上表示出來.
![]()
(3)解不等式組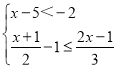 ,并求出不等式組的整數解.
,并求出不等式組的整數解.
(4)因式分解
①2a3b﹣8ab3
②6a(b-a) 2﹣2(a-b) 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“保護好環境,拒絕冒黑煙”荊州市公交公司將淘汰一條線路上“冒黑煙”較嚴重的公交車,計劃購買![]() 型和
型和![]() 型兩種環保節能公交車
型兩種環保節能公交車![]() 輛,若購買
輛,若購買![]() 型公交車
型公交車![]() 輛,
輛,![]() 型公交車
型公交車![]() 輛,共需
輛,共需![]() 萬元,若購買
萬元,若購買![]() 型公交車
型公交車![]() 輛,
輛,![]() 型公交車
型公交車![]() 輛,共需
輛,共需![]() 萬元.
萬元.
(1)求購買購買![]() 型和
型和![]() 型公交車每輛多少錢?
型公交車每輛多少錢?
(2)預計在該線路上![]() 型和
型和![]() 型公交車每輛年均載客量分別為
型公交車每輛年均載客量分別為![]() 萬人次和
萬人次和![]() 萬人次,若該公司購買
萬人次,若該公司購買![]() 型和
型和![]() 型公交車的總費用不超過
型公交車的總費用不超過![]() 萬元,且確保這
萬元,且確保這![]() 輛公交車在該線路上的年平均載客總和不少于
輛公交車在該線路上的年平均載客總和不少于![]() 萬人次,則該公司有哪幾種購車方案?
萬人次,則該公司有哪幾種購車方案?
(3)在(2)的條件下,哪種購車方案總費用最少?最少費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中每個小格子的邊長均為![]() 個單位長度,
個單位長度,![]() 的三個頂點和點
的三個頂點和點![]() 都在方格紙的格點上,
都在方格紙的格點上,
(1)若將![]() 平移,使點
平移,使點![]() 恰好落在平移后得到的
恰好落在平移后得到的![]() 的內部,則符合要求的三角形能畫出_______個,請在方格紙中畫出符合要求的一個三角形;
的內部,則符合要求的三角形能畫出_______個,請在方格紙中畫出符合要求的一個三角形;
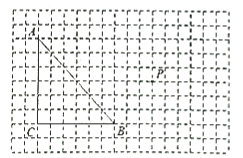
(2)在(1)的條件下,若連接對應點![]() 、
、![]() ,則這兩條線段的位置關系是______;
,則這兩條線段的位置關系是______;
(3)畫一條直線![]() ,將
,將![]() 分成兩個面積相等的三角形.
分成兩個面積相等的三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】溫州市在今年三月份啟動實施“明眸皓齒”工程.根據安排,某校對于學生使用電子產品的一周用時情況進行抽樣調查,繪制成以下頻數分布直方圖.請根據圖中提供的信息,解答下列問題.

(1)這次共抽取了 名學生進行調查.
(2)用時在2.45~3.45小時這組的頻數是_ , 頻率是_ .
(3)如果該校有1000名學生,請估計一周電子產品用時在0.45~3.45小時的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
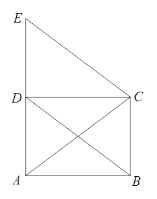
【題目】已知:如圖,四邊形ABCD是平行四邊形,CE∥BD交AD的延長線于點E,CE=AC.
(1)求證:四邊形ABCD是矩形;
(2)若AB=4,AD=3,求四邊形BCED的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com