
【題目】在一個不透明袋子中有1個紅球、1 個綠球和n個白球,這些球除顏色外都相同.
(1)從袋中隨機摸出1個球,記錄下顏色后放回袋子中并攪勻,不斷重復該試驗.發現摸到白球的頻率穩定在0.75,則n的值為;
(2)當n=2時,把袋中的球攪勻后任意摸出2個球,求摸出的2個球顏色不同的概率.
【答案】
(1)6
(2)解:任意摸出2個球,共有12種等可能的結果,即(紅,綠)、(紅,白1)、(紅,白2)、(綠,紅)、(綠,白1)、(綠,白1)、(白1,紅)、(白1,綠)、(白1,白2)、(白2,紅)、(白2,綠)、(白2,白1),
其中2個球顏色不同的結果有10種,所以所求概率為 ![]() .
.
【解析】(1)根據白球的頻率穩定在0.75附近得到白球的概率約為0.75,根據白球個數確定出總個數,進而確定出黑球個數;(2)將所有等可能的結果列舉出來,利用概率公式求解即可.
【考點精析】本題主要考查了列表法與樹狀圖法和用頻率估計概率的相關知識點,需要掌握當一次試驗要設計三個或更多的因素時,用列表法就不方便了,為了不重不漏地列出所有可能的結果,通常采用樹狀圖法求概率;在同樣條件下,做大量的重復試驗,利用一個隨機事件發生的頻率逐漸穩定到某個常數,可以估計這個事件發生的概率才能正確解答此題.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中數學 來源: 題型:
【題目】如圖,有一個不定的正方形ABCD,它的兩個相對的頂點A,C分別在邊長為1的正六邊形一組對邊上,另外兩個頂點B,D在正六邊形內部(包括邊界),則正方形邊長a的取值范圍是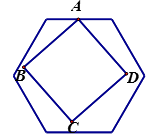
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一個不定的正方形ABCD,它的兩個相對的頂點A,C分別在邊長為1的正六邊形一組對邊上,另外兩個頂點B,D在正六邊形內部(包括邊界),則正方形邊長a的取值范圍是
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】交通工程學理論把在單向道路上行駛的汽車看成連續的液體,并用流量、速度、密度三個概念描述車流的基本特征。其中流量q(輛/小時)指單位時間內通過道路指定斷面的車輛數;速度v(千米/小時)指通過道路指定斷面的車輛速度;密度(輛/千米)指通過道路指定斷面單位長度內的車輛數,為配合大數據治堵行動,測得某路段流量q與速度v之間的部分數據如下表:
速度v(千米/小時) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量q(輛/小時) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根據上表信息,下列三個函數關系式中,刻畫q,v關系最準確的是(只需填上正確答案的序號)① ![]() ②
② ![]() ③
③ ![]()
(2)請利用(1)中選取的函數關系式分析,當該路段的車流速為多少時,流量達到最大?最大流量是多少?
(3)已知q,v,k滿足 ![]() ,請結合(1)中選取的函數關系式繼續解決下列問題:
,請結合(1)中選取的函數關系式繼續解決下列問題:
①市交通運行監控平臺顯示,當 ![]() 時道路出現輕度擁堵,試分析當車流密度k在什么范圍時,該路段出現輕度擁堵;
時道路出現輕度擁堵,試分析當車流密度k在什么范圍時,該路段出現輕度擁堵;
②在理想狀態下,假設前后兩車車頭之間的距離d(米)均相等,求流量q最大時d的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數的圖象l經過點A(2,5),B(-4,-1)兩點.
(1)求一次函數表達式.
(2)若點E在x軸上,且E(2,O),點C為直線l與x軸的交點,求△CDE的面積.
(3)你能求出點E到直線l的距離嗎?
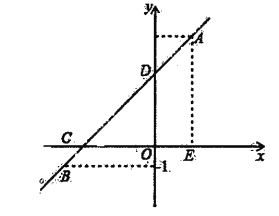
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景點的門票價格如表:
購票人數/人 | 1~50 | 51~100 | 100以上 |
每人門票價/元 | 12 | 10 | 8 |
某校七年級(1)、(2)兩班計劃去游覽該景點,其中(1)班人數少于50人,(2)班人數多于50人且少于100人,如果兩班都以班為單位單獨購票,則一共支付1118元;如果兩班聯合起來作為一個團體購票,則只需花費816元.
(1)兩個班各有多少名學生?
(2)團體購票與單獨購票相比較,兩個班各節約了多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,已知⊙O的半徑為1,菱形ABCD的三個頂點A、B、D在⊙O上,且CD與⊙O相切.
(1)求證:BC與⊙O相切;
(2)求陰影部分面積. 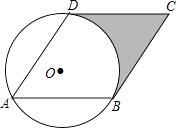
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE與FC會平行嗎?說明理由.
(2)AD與BC的位置關系如何?為什么?
(3)BC平分∠DBE嗎?為什么.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com