
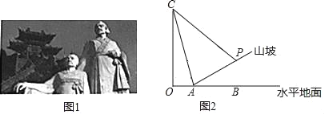
【題目】某游客計劃測量這座塑像的高度,(如圖1),由于游客無法直接到達塑像底部,因此該游客計劃借助坡面高度來測量塑像的高度;如圖2,在塑像旁山坡坡腳A處測得塑像頭頂C的仰角為75°,當從A處沿坡面行走10米到達P處時,測得塑像頭頂C的仰角剛好為45°,已知山坡的坡度i=1:3,且O,A,B在同一直線上,求塑像的高度.(側傾器高度忽略不計,結果精確到0.1米,參考數據:cos75°≈0.3,tan75°≈3.7,![]() ,
,![]() ,
,![]() )
)
【答案】塑像的高度約為 17.5 米.
【解析】
過點P作PE⊥OB于點E,PF⊥OC于點F,設PE=x,則AE=3x,在Rt△AEP中根據勾股定理得PE,在Rt△AOC中,由tan75°求得m的值,繼而可得答案.
過點 P 作 PE⊥OB 交 OB 于點 E,PF⊥OC 交 OC 于點 F,
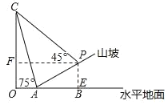
∵i=1:3,AP=10,
設 PE=x,則 AE=3x,
在 Rt△AEP 中,x2+(3x)2=102,
解得:![]() 或
或![]() (舍),
(舍),
∴![]() ,則
,則![]() ,
,
∵∠CPF=∠PCF=45°,
∴CF=PF,
設 CF=PF=m 米,則![]() 米,
米,![]() 米,
米,
在 Rt△AOC 中,![]() 即
即![]()
解得:m≈14.3,
∴![]() 米,
米,
答:塑像的高度約為 17.5 米.


科目:初中數學 來源: 題型:
【題目】《歌手—當打之年》是湖南衛視最受歡迎的娛樂節目,奇襲挑戰賽在每周五晚準時進行,7名主打歌手進行比賽的同時還要接受1名奇襲歌手挑戰.近期即將進行終極奇襲戰,奇襲歌手艾熱將挑戰徐佳瑩(女)、米希亞(女)、蕭敬騰、華晨宇、周深、聲入人心男團、旅行團樂隊.
(1)當主持人詢問艾熱準備奇襲哪位歌手時,艾熱透露“希望和男性嗓音去比試”,那周深被奇襲的概率是 ;
(2)7名主打歌手比賽的上場順序是通過抽簽方式進行,若已經知道前4位歌手的上場順序,還有華晨宇、米希亞、周深不知道,那么華晨宇和周深兩位是相鄰出場的概率是多少.(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年湖南省進入高中學習的學生三年后將面對新高考,高考方案與高校招生政策都將有重大變化。某部門為了了解政策的宣傳情況,對某初級中學學生進行了隨機抽樣調查,根據學生對政策的了解程度由高到低分為A,B,C,D四個等級,并對調查結果分析后繪制了如下兩幅圖不完整的統計圖。請你根據圖中提供的信息完成下列問題:
(1)求被調查學生的人數,并將條形統計圖補充完整;
(2)求扇形統計圖中的A等對應的扇形圓心角的度數;
(3)已知該校有1500名學生,估計該校學生對政策內容了解程度達到A等的學生有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“禹州鈞瓷”名揚天下,某網店專門銷售某種品牌的鈞瓷花瓶,成本為40元/件,每天銷量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間存在一次函數關系,如圖所示.
(元)之間存在一次函數關系,如圖所示.
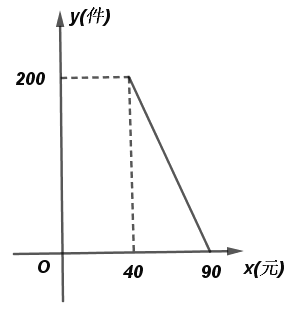
(1)求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(2)如果規定每天鈞瓷花瓶的銷售量不低于120件,當銷售單價為多少元時,每天獲取的利潤最大,最大利潤是多少元?
(3)該網店店主熱心公益事業,決定從每天的銷售利潤中捐出100元給希望工程,為了保證捐款后每天剩余利潤不低于2000元,試確定該鈞瓷花瓶銷售單價的范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
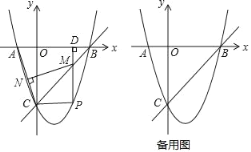
【題目】如圖,在平面直角坐標系中,拋物線y=x2+bx+c交x軸于A,B兩點,交y軸于點C,直線y=x﹣3經過B,C兩點.
(1)求拋物線的解析式;
(2)點P是第四象限內拋物線上的動點,過點P作PD⊥x軸于點D,交直線BC于點M,連接AC,過點M作MN⊥AC于點N,設點P的橫坐標為t.
①求線段MN的長d與t之間的函數關系式(不要求寫出自變量t的取值范圍);
②點Q是平面內一點,是否存在一點P,使以B,C,P,Q為頂點的四邊形為矩形?若存在,請直接寫出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a>0)經過點M(﹣1,2)和點N(1,﹣2),則下列說法錯誤的是( )
A.a+c=0
B.無論a取何值,此二次函數圖象與x軸必有兩個交點,且函數圖象截x軸所得的線段長度必大于2
C.當函數在x<![]() 時,y隨x的增大而減小
時,y隨x的增大而減小
D.當﹣1<m<n<0時,m+n<![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在多項式的乘法公式中,完全平方公式![]() 是其中重要的一個.
是其中重要的一個.
(1)請補全完全平方公式的推導過程:
![]() ,
,
![]() ,
,
![]() .
.
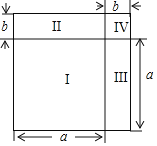
(2)如圖,將邊長為![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,請你結合圖給出完全平方公式的幾何解釋.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,請你結合圖給出完全平方公式的幾何解釋.
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
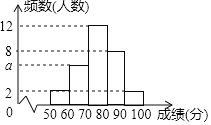
【題目】為了解某次“小學生書法比賽”的成績情況,隨機抽取了30名學生的成績進行統計,并將統計情況繪成如圖所示的頻數分布直方圖,己知成績x(單位:分)均滿足“50≤x<100”.根據圖中信息回答下列問題:
(1)圖中a的值為 ;
(2)若要繪制該樣本的扇形統計圖,則成績x在“70≤x<80”所對應扇形的圓心角度數為 度;
(3)此次比賽共有300名學生參加,若將“x≥80”的成績記為“優秀”,則獲得“優秀“的學生大約有 人:
(4)在這些抽查的樣本中,小明的成績為92分,若從成績在“50≤x<60”和“90≤x<100”的學生中任選2人,請用列表或畫樹狀圖的方法,求小明被選中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com