
【題目】二次函數y=ax2+bx+c的自變量x與函數值y的部分對應值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根據表格中的信息,完成下列各題:
(1)當x=3時,y=________;
(2)當x=_____時,y有最________值為________;
(3)若點A(x1,y1)、B(x2,y2)是該二次函數圖象上的兩點,且﹣1<x1<0,1<x2<2,試比較兩函數值的大小:y1________y2 ;
(4)若自變量x的取值范圍是0≤x≤5,則函數值y的取值范圍是________.
【答案】(1)﹣1;(2)1、小、﹣2;(3)>;(4)﹣2≤y≤2
【解析】
(1)由表中給出的三組數據,列方程組求得二次函數的解析式,再求出x=3時,y的值;
(2)實際上是求二次函數的頂點坐標;
(3)求得拋物線與x軸的兩個交點坐標,在對稱軸的左側,y隨x的增大而減小;在對稱軸的右側,y隨x的增大而增大;再進行判斷即可;
(4)根據拋物線的頂點,當x=5時,y最大,當x=1時,y最小.
(1)由表得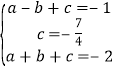 ,解得:
,解得: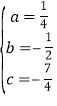 ,∴二次函數的解析式為y=
,∴二次函數的解析式為y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ,當x=3時,y=
,當x=3時,y=![]() =﹣1.
=﹣1.
(2)將y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 配方得:y=
配方得:y=![]() (x﹣1)2﹣2.
(x﹣1)2﹣2.
∵a=![]() >0,∴函數有最小值,當x=1時,最小值為﹣2.
>0,∴函數有最小值,當x=1時,最小值為﹣2.
(3)令y=0,則x=±2![]() +1,拋物線與x軸的兩個交點坐標為(2
+1,拋物線與x軸的兩個交點坐標為(2![]() +1,0)(﹣2
+1,0)(﹣2![]() +1,0)
+1,0)
∵﹣1<x1<0,1<x2<2,∴x1到1的距離大于x2到1的距離,∴y1>y2.
(4)∵拋物線的頂點為(1,﹣2),∴當x=5時,y最大,即y=2;當x=1時,y最小,即y=﹣2,∴函數值y的取值范圍是﹣2≤y≤2.
故答案為:﹣1;1、小、﹣2;>;﹣2≤y≤2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知BD,CE是△ABC的兩條高,直線BD,CE相交于點H.

(1)若∠BAC=100°,求∠DHE的度數;
(2)若△ABC中∠BAC=50°,直接寫出∠DHE的度數是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
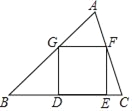
【題目】如圖,已知正方形DEFG的頂點D、E在△ABC的邊BC上,頂點G、F分別在邊AB、AC上,如果BC=5,△ABC的面積是10,那么這個正方形的邊長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
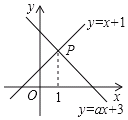
【題目】如圖,已知函數y=x+1和y=ax+3的圖象交于點P,點P的橫坐標為1,
(1)關于x,y的方程組![]() 的解是 ;
的解是 ;
(2)a= ;
(3)求出函數y=x+1和y=ax+3的圖象與x軸圍成的幾何圖形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
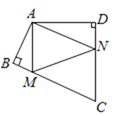
【題目】如圖,在四邊形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分別找一點M,N,使三角形AMN周長最小時,則∠MAN的度數為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩種機器人都被用來搬運化工原料,A型機器人比B型機器人每小時多搬運30kg,A型機器人搬運900kg與B型機器人搬運600kg所用時間相等,兩種機器人每小時分別搬運多少化工原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋中裝有![]() 個紅球和
個紅球和![]() 個白球,每個球除顏色外,其余特征均相同.
個白球,每個球除顏色外,其余特征均相同.
![]() 任意摸出
任意摸出![]() 個球,摸出紅球的概率是多少?
個球,摸出紅球的概率是多少?
![]() 任意摸出
任意摸出![]() 個球,摸到紅球小明勝,摸出白球小剛勝,這個游戲公平嗎?如果不公平,請你在此基礎上設計一個公平的游戲,并說明你的設計理由.
個球,摸到紅球小明勝,摸出白球小剛勝,這個游戲公平嗎?如果不公平,請你在此基礎上設計一個公平的游戲,并說明你的設計理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是BC的中點,AB⊥BC,DC⊥BC,AE平分∠BAD,下列結論:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四個結論中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com