
【題目】一個電子跳蚤從數軸的原點出發,連續不斷地一左一右來回跳動(第一次向左跳),跳動的距離依次為![]() ,
,![]() ,
,![]() ,
,![]() …
…
(1)如果![]() 是正整數,那么第
是正整數,那么第![]() 次跳動的距離是______;
次跳動的距離是______;
(2)第![]() 次跳動的落點位置所對應的有理數是______;
次跳動的落點位置所對應的有理數是______;
(3)第![]() 次跳動后所處位置在原點的______側;
次跳動后所處位置在原點的______側;
(4)①相對于出發點,電子跳蚤第一次跳記作![]() (向左跳),第二次跳記作
(向左跳),第二次跳記作![]() (向右跳),以此類推,如果
(向右跳),以此類推,如果![]() 是正整數,那么第
是正整數,那么第![]() 次記作______;
次記作______;
②會不會有相鄰兩次跳動的落點位置在原點的同側?
【答案】(1)n;(2)-3;(3)右;(4)①![]() ,②不會,見解析
,②不會,見解析
【解析】
(1)根據題意可得第n次跳動的距離為n;(2)利用算式-1+2-3+4-5= -3可得;(3)利用算式-1+2-3+4-5+…+100= 50可得;(4)①根據奇、偶數的表示方法可得;②列式計算,根據計算結果分析判斷.
解:(1)∵第一、二、三、四次跳動的距離為![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴第n次跳動的距離為![]() ;
;
(2)根據題意得,![]() ,
,
∴第![]() 次跳動的落點位置所對應的有理數是-3;
次跳動的落點位置所對應的有理數是-3;
(3)根據題意得,![]() ,
,
∴第![]() 次跳動后所處位置在原點的右側;
次跳動后所處位置在原點的右側;
(4)①根據題意可得,當n(n為正整數)為奇數時跳到原點左側,記為n的相反數-n,當n(n為正整數)為偶數時跳到原點右側,記為n,
∴當![]() 是正整數,第
是正整數,第![]() 次記作
次記作![]() .
.
②不會
求和:![]()
當![]() 為奇數時,原式
為奇數時,原式![]()
當![]() 為偶數時,原式
為偶數時,原式![]()
由此可知,從兩個加數起,每增加一個加數,和的符號都會改變,故不會出現相鄰兩次跳動的落點位置在原點的同側.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:初中數學 來源: 題型:
【題目】暑假到了,即將迎來手機市場的銷售旺季.某商場銷售甲、乙兩種品牌的智能手機,這兩種手機的進價和售價如下表所示:
甲 | 乙 | |
進價(元/部) | 4000 | 2500 |
售價(元/部) | 4300 | 3000 |
該商場計劃投入15.5萬元資金,全部用于購進兩種手機若干部,期望全部銷售后可獲毛利潤不低于2萬元.(毛利潤=(售價﹣進價)×銷售量)
(1)若商場要想盡可能多的購進甲種手機,應該安排怎樣的進貨方案購進甲乙兩種手機?
(2)通過市場調研,該商場決定在甲種手機購進最多的方案上,減少甲種手機的購進數量,增加乙種手機的購進數量.已知乙種手機增加的數量是甲種手機減少的數量的2倍,而且用于購進這兩種手機的總資金不超過16萬元,該商場怎樣進貨,使全部銷售后獲得的毛利潤最大?并求出最大毛利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A地在數軸上表示的數為-16,AB兩地相距50個單位長度.小明從A地出發去B地,以每分鐘2個單位長度的速度行進,第一次他向左1單位長度,第二次向右2單位長度,第三次再向左3單位長度,第四次又向右4單位長度…,按此規律行進.
![]()
(1)求出B地在數軸上表示的數;
(2)若B地在原點的右側,經過第8次行進后小明到達點P,此時點P與點B相距幾個單位長度?8次運動完成后一共經過了幾分鐘?
(3)若經過n次(n為正整數)行進后,小明到達點Q,請你直接寫出:點Q在數軸上表示的數應如何表示?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年本市蜜桔大豐收,某水果商銷售一種蜜桔,成本價為10元/千克,已知銷售價不低于成本價,且物價部門規定這種產品的銷售價不高于18元/千克,市場調查發現,該產品每天的銷售量y(千克)與銷售價x(元/千克)之間的函數關系如圖所示:
(1)求y與x之間的函數關系式;
(2)該經銷商想要每天獲得150元的銷售利潤,銷售價應定為多少?
(銷售利潤=銷售價-成本價)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,已知AB=6,BC=9, ![]() .對角線AC、BD交于點O.動點P在邊AB上,⊙P經過點B,交線段PA于點E.設BP= x.
.對角線AC、BD交于點O.動點P在邊AB上,⊙P經過點B,交線段PA于點E.設BP= x.
(1)求AC的長;
(2)設⊙O的半徑為y,當⊙P與⊙O外切時,求y關于x的函數解析式,并寫出定義域;
(3)如果AC是⊙O的直徑,⊙O經過點E,求⊙O與⊙P的圓心距OP的長.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(﹣2,0),點B的坐標為(0,n),以點B為直角頂點,點C在第二象限內,作等腰直角△ABC.
(1)點C的坐標為 (用字母n表示)
(2)如果△ABC的面積為5.5,求n的值;
(3)在(2)的條件下,坐標平面內是否存在一點M,使以點M、A、B為頂點組成的三角形與△ABC全等?如果存在畫出符合要求的圖形,求出點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
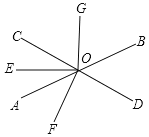
【題目】如圖,直線AB與CD相交于O,OE是∠AOC的平分線,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度數;
(2)求∠EOF與∠BOG是否相等?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,點E在CD邊上,點F在DC延長線上,AE=BF.
(1)求證:四邊形ABFE是平行四邊形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com