
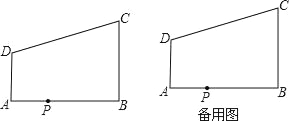
【題目】如圖,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,點P為AB邊上一動點,若△PAD與△PBC是相似三角形,求AP的長.
【答案】AP=![]() 或AP=2或AP=6
或AP=2或AP=6
【解析】試題分析:由AD//BC, ∠B=90°,可證∠PAD=∠PBC=90°, 又由AB=8,AD=3,BC=4,設AP的長為x,則BP長為8-x,然后分別從APD∽△BPC與△APD∽△BCP去分析,利用相似三角形的對應邊成比例求解即可求得答案.
試題解析:∵ AB⊥BC,
∴ ∠B=90°,
∵ AD∥BC,
∴ ∠A=180°﹣∠B=90°,
∴ ∠PAD=∠PBC=90°,
AB=8,AD=3,BC=4,
設AP的長為x,則BP長為8﹣x,
若AB邊上存在P點,使△PAD與△PBC相似,那么分兩種情況:
若△APD∽△BPC,則AP:BP=AD:BC,即x:(8﹣x)=3:4,
解得x=![]() ,
,
若△APD∽△BCP,則AP:BC=AD:BP,即x:4=3:(8﹣x),
解得x=2或x=6,
所以AP=![]() 或AP=2或AP=6.
或AP=2或AP=6.


科目:初中數學 來源: 題型:
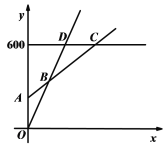
【題目】某水上樂園普通票價20元/張,假期為了促銷,新推出兩種優惠卡:貴賓卡售價600元/張,每次憑卡不再收費;會員卡售價200元/張,每次憑卡另收10元.暑期普通票正常出售,兩種優惠卡僅限暑期使用,不限次數.設游泳x次時,所需總費用為y元.
(1)分別寫出假期選擇會員卡、普通票消費時,y與x之間的函數關系式;
(2)在同一個坐標系中,若三種消費方式對應的函數圖象如圖所示,請求出點A、B、C、D的坐標,并直接寫出選擇哪種消費方式更合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義運算a![]() b=a(1-b),下面給出了關于這種運算的四個結論:
b=a(1-b),下面給出了關于這種運算的四個結論:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,則(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,則a=0.
b=0,則a=0.
其中正確結論的序號是 (填上你認為所有正確結論的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
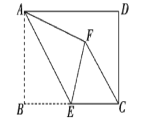
【題目】如圖,在矩形ABCD中,AB=4,BC=6,點E為BC的中點,將△ABE沿AE折疊,使點B落在矩形內點F處,連接CF,則CF的長度為_____
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1=∠2,要說明△ABD≌△ACD,還需從下列條件中選一個,錯誤的選法是( )
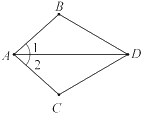
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校組織![]() 名同學和
名同學和![]() 名教師參加校外學習交流活動現打算選租大、小兩種客車,大客車載客量為
名教師參加校外學習交流活動現打算選租大、小兩種客車,大客車載客量為![]() 人/輛,小客車載客量為
人/輛,小客車載客量為![]() 人/輛
人/輛
(1)學校準備租用![]() 輛客車,有幾種租車方案?
輛客車,有幾種租車方案?
(2)在(1)的條件下,若大客車租金為![]() 元/輛,小客車租金為
元/輛,小客車租金為![]() 元/輛,哪種租車方案最省錢?
元/輛,哪種租車方案最省錢?
(3)學校臨時增加![]() 名學生和
名學生和![]() 名教師參加活動,每輛大客車有2名教師帶隊,每輛小客車至少有
名教師參加活動,每輛大客車有2名教師帶隊,每輛小客車至少有![]() 名教師帶隊.同學先坐滿大客車,再依次坐滿小客車,最后一輛小客車至少要有
名教師帶隊.同學先坐滿大客車,再依次坐滿小客車,最后一輛小客車至少要有![]() 人,請你幫助設計租車方案
人,請你幫助設計租車方案
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD折疊,使點D與點B重合,點C落在C′處,折痕為EF,若AB=1,BC=2,則△ABE和△BC′F的周長之和為( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com