
【題目】閱讀理解:
(閱讀材料)
在數(shù)軸上,通常用“兩數(shù)的差”來(lái)表示“數(shù)軸上兩點(diǎn)的距離”如圖1中三條線段的
長(zhǎng)度可表示為:![]() ,
,![]() 結(jié)論:數(shù)軸上任意兩點(diǎn)
結(jié)論:數(shù)軸上任意兩點(diǎn)
表示的數(shù)為分別![]() ,則這兩個(gè)點(diǎn)間的距離為
,則這兩個(gè)點(diǎn)間的距離為![]() (即:用較大的數(shù)去減較小的數(shù))
(即:用較大的數(shù)去減較小的數(shù))
![]()
(理解運(yùn)用)
根據(jù)閱讀材料完成下列各題:
(1)如圖2, ![]() 分別表示數(shù)
分別表示數(shù)![]() ,求線段
,求線段![]() 的長(zhǎng);
的長(zhǎng);
![]()
(2)若在直線![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]() ,求點(diǎn)
,求點(diǎn)![]() 對(duì)應(yīng)的數(shù)值.
對(duì)應(yīng)的數(shù)值.
(3)![]() 兩點(diǎn)分別從
兩點(diǎn)分別從![]() 同時(shí)出發(fā)以3個(gè)單位、2個(gè)單位長(zhǎng)度的速度沿?cái)?shù)軸向右運(yùn)動(dòng),求當(dāng)點(diǎn)
同時(shí)出發(fā)以3個(gè)單位、2個(gè)單位長(zhǎng)度的速度沿?cái)?shù)軸向右運(yùn)動(dòng),求當(dāng)點(diǎn)![]() 重合時(shí),它們運(yùn)動(dòng)的時(shí)間;
重合時(shí),它們運(yùn)動(dòng)的時(shí)間;
(4)在(3)的條件下,求當(dāng)![]() 時(shí),它們運(yùn)動(dòng)的時(shí)間.
時(shí),它們運(yùn)動(dòng)的時(shí)間.
【答案】(1) 線段![]() 的長(zhǎng)為8;(2)
的長(zhǎng)為8;(2)![]() 時(shí),點(diǎn)對(duì)應(yīng)的數(shù)值為5或9;(3)運(yùn)動(dòng)時(shí)間為
時(shí),點(diǎn)對(duì)應(yīng)的數(shù)值為5或9;(3)運(yùn)動(dòng)時(shí)間為![]() 秒時(shí),
秒時(shí),![]() 重合;(4)運(yùn)動(dòng)時(shí)間為4或12小時(shí),
重合;(4)運(yùn)動(dòng)時(shí)間為4或12小時(shí),![]() .
.
【解析】
(1) 由題意,直接觀察數(shù)軸和定義代入即可求出線段![]() 的長(zhǎng);
的長(zhǎng);
(2)根據(jù)題意設(shè)點(diǎn)![]() 對(duì)應(yīng)的數(shù)值為
對(duì)應(yīng)的數(shù)值為![]() ,分當(dāng)點(diǎn)
,分當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 左側(cè)時(shí)以及當(dāng)點(diǎn)
左側(cè)時(shí)以及當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 右側(cè)時(shí)列方程求解即可;
右側(cè)時(shí)列方程求解即可;
(3)根據(jù)題意設(shè)運(yùn)動(dòng)時(shí)間為![]() 秒時(shí)
秒時(shí)![]() 重合用含t的代數(shù)式表示出M、N進(jìn)行分析;
重合用含t的代數(shù)式表示出M、N進(jìn)行分析;
(4)由題意設(shè)運(yùn)動(dòng)時(shí)間為![]() 秒時(shí),
秒時(shí),![]() ,分當(dāng)點(diǎn)
,分當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 左側(cè)時(shí)以及當(dāng)點(diǎn)
左側(cè)時(shí)以及當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 右側(cè)時(shí)進(jìn)行分析求解.
右側(cè)時(shí)進(jìn)行分析求解.
解:(1)由題意得,線段![]() 的長(zhǎng)為:
的長(zhǎng)為:![]() ,
,
答:線段![]() 的長(zhǎng)為8.
的長(zhǎng)為8.
(2)設(shè)點(diǎn)![]() 對(duì)應(yīng)的數(shù)值為
對(duì)應(yīng)的數(shù)值為![]()
(ⅰ)當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 左側(cè)時(shí),
左側(cè)時(shí),
![]()
因?yàn)?/span>![]()
所以![]()
解得![]()
(ⅱ)當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 右側(cè)時(shí)
右側(cè)時(shí)
![]()
因?yàn)?/span>![]()
所以![]()
解得![]()
答:![]() 時(shí),點(diǎn)對(duì)應(yīng)的數(shù)值為5或9.
時(shí),點(diǎn)對(duì)應(yīng)的數(shù)值為5或9.
(3)設(shè)運(yùn)動(dòng)時(shí)間為![]() 秒時(shí),
秒時(shí),![]() 重合
重合
![]() 點(diǎn)對(duì)應(yīng)數(shù)值表示為
點(diǎn)對(duì)應(yīng)數(shù)值表示為![]() ,
,![]() 點(diǎn)對(duì)應(yīng)數(shù)值表示為
點(diǎn)對(duì)應(yīng)數(shù)值表示為![]()
由題意得![]()
解得![]()
答:運(yùn)動(dòng)時(shí)間為![]() 秒時(shí),
秒時(shí),![]() 重合.
重合.
(4)設(shè)運(yùn)動(dòng)時(shí)間為![]() 秒時(shí),
秒時(shí),![]() ,
,
(ⅰ)當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 左側(cè)時(shí),
左側(cè)時(shí),
由(3)有![]()
解得:![]()
(ⅱ)當(dāng)點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 右側(cè)時(shí)
右側(cè)時(shí)
![]()
![]()
答:運(yùn)動(dòng)時(shí)間為4或12小時(shí),![]() .
.


 開(kāi)心練習(xí)課課練與單元檢測(cè)系列答案
開(kāi)心練習(xí)課課練與單元檢測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
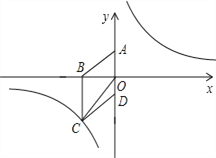
【題目】如圖,在平面直角坐標(biāo)系中,已知四邊形ABCD為菱形,且![]() (0,3)、
(0,3)、![]() (﹣4,0).
(﹣4,0).
(1)求經(jīng)過(guò)點(diǎn)![]() 的反比例函數(shù)的解析式;
的反比例函數(shù)的解析式;
(2)設(shè)![]() 是(1)中所求函數(shù)圖象上一點(diǎn),以
是(1)中所求函數(shù)圖象上一點(diǎn),以![]() 頂點(diǎn)的三角形的面積與△COD的面積相等.求點(diǎn)P的坐標(biāo).
頂點(diǎn)的三角形的面積與△COD的面積相等.求點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+![]() ab+
ab+![]() .
.
(1)a=﹣1,b=﹣2時(shí),求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值與a的取值無(wú)關(guān),求b的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
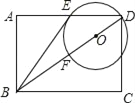
【題目】已知:如圖,在矩形ABCD中,點(diǎn)O在對(duì)角線BD上,以OD的長(zhǎng)為半徑的⊙O與AD,BD分別交于點(diǎn)E、點(diǎn)F,且∠ABE=∠DBC.
(1)判斷直線BE與⊙O的位置關(guān)系,并證明你的結(jié)論;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半徑.
,CD=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
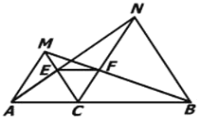
【題目】已知:如圖,點(diǎn)C為線段AB上一點(diǎn),△ACM, △CBN都是等邊三角形,AM=AC=CM,BC=CN=BN,∠ACM=∠BCN=60°,AN交MC于點(diǎn)E,BM交CN于點(diǎn)F.
(1)求證:AN=BM;
(2)求證:判斷△CEF形狀
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
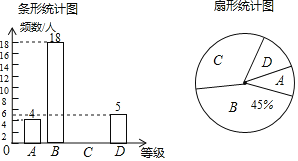
【題目】某學(xué)校為了解今年八年級(jí)學(xué)生足球運(yùn)球的掌握情況,隨機(jī)抽取部分八年級(jí)學(xué)生足球運(yùn)球的測(cè)試成績(jī)作為一個(gè)樣本,按A、B、C、D四個(gè)等級(jí)進(jìn)行如圖不完整的統(tǒng)計(jì)圖根據(jù)所給信息,解答以下問(wèn)題:
(1)在扇形統(tǒng)計(jì)圖中,C對(duì)應(yīng)的扇形的圓心角是 度;
(2)補(bǔ)全條形統(tǒng)計(jì)圖、扇形統(tǒng)計(jì)圖;
(3)該校八年級(jí)有300名學(xué)生,請(qǐng)估計(jì)足球運(yùn)球測(cè)試成績(jī)達(dá)到A級(jí)的學(xué)生有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
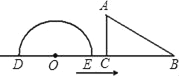
【題目】如圖,已知半圓O的直徑DE=12cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm,半圓O以2cm/s的速度從左向右運(yùn)動(dòng),在運(yùn)動(dòng)過(guò)程中,點(diǎn)D、E始終在直線BC上.設(shè)運(yùn)動(dòng)時(shí)間為t(s),當(dāng)t=0s時(shí),半圓O在△ABC的左側(cè),OC=8cm.
(1)當(dāng)t為何值時(shí),△ABC的一邊所在直線與半圓O所在的圓相切?
(2)當(dāng)△ABC的一邊所在直線與半圓O所在的圓相切時(shí),如果半圓O與直線DE圍成的區(qū)域與△ABC三邊圍成的區(qū)域有重疊部分,求重疊部分的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
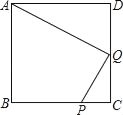
【題目】如圖,P是正方形ABCD邊BC上的一點(diǎn),且BP=3PC,Q是CD中點(diǎn).
(1)求證:△ADQ∽△QCP.
(2)試問(wèn):AQ與PQ有什么關(guān)系(位置與數(shù)量)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,四邊形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求證:BD⊥CB;
(2)求四邊形 ABCD 的面積;
(3)如圖 2,以 A 為坐標(biāo)原點(diǎn),以 AB、AD所在直線為 x軸、y軸建立直角坐標(biāo)系,
點(diǎn)P在y軸上,若 S△PBD=![]() S四邊形ABCD,求 P的坐標(biāo).
S四邊形ABCD,求 P的坐標(biāo).

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com