
【題目】如圖,在![]() 中,以
中,以![]() 為直徑的
為直徑的![]() 經(jīng)過點
經(jīng)過點![]() 過點
過點![]() 作
作![]() 的切線
的切線![]() 點
點![]() 是
是![]() 上不與點
上不與點![]() 重合的一個動點,連接
重合的一個動點,連接![]() .
.
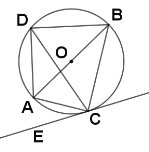
![]() 求證:
求證:![]() ;
;
![]() 填空:
填空:
![]() 當(dāng)
當(dāng)![]() _ 時,
_ 時,![]() 為等腰直角三角形:
為等腰直角三角形:
![]() 當(dāng)
當(dāng)![]() 時,四邊形
時,四邊形![]() 為菱形.
為菱形.
【答案】![]() 見解析;
見解析;![]() ①45°②120°
①45°②120°
【解析】
(1)連接OC.根據(jù)等腰三角形的性質(zhì)得到∠OCB=∠OBC,根據(jù)平行線的性質(zhì)得到∠ACB=90°.再根據(jù)切線的性質(zhì)定理及圓周角定理即可得到結(jié)論;
(2)①根據(jù)圓的對稱性由BD=AD可得弧BD=弧AD,再由圓周角定理得∠DCB=∠DCA,進(jìn)而得解;
②由菱形可得OD=AD,結(jié)合OD=OA,證得△OAD為等邊三角形,則∠OAD=60°,最后根據(jù)圓周角定理即可得解.
解:![]() 如圖,連接
如圖,連接![]()
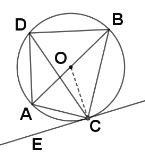
![]()
![]()
![]() 為
為![]() 的直徑,
的直徑,
![]()
![]() ,
,
![]() 是
是![]() 的切線,
的切線,
![]()
![]()
![]()
![]()
![]()
(2)①∵![]() 為等腰直角三角形,
為等腰直角三角形,
∴AD=DB,
∴弧AD=弧DB,
∴∠ACD=∠DCB=![]() ∠ACB,
∠ACB,
∵∠ACB=90°,
∴∠DCB=45°,
②∵四邊形![]() 為菱形,
為菱形,
∴OD=AD,
又∵OD=OA,
∴OD=OA=AD,
∴△AOD為等邊三角形,
∴∠OAD=60°,
∵∠OAD=![]() ∠DOB,
∠DOB,
∴∠DOB=120°.


 長江作業(yè)本同步練習(xí)冊系列答案
長江作業(yè)本同步練習(xí)冊系列答案 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點P是BA延長線上一點,PC是⊙O的切線,切點為C,過點B作BD⊥PC交PC的延長線于點D,連接BC.求證:
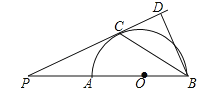
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角三角形ABC中,∠C=90°,AC=2,BC=2![]() ,點O是邊AB上的一個動點,以點O為圓心,OA為半徑作⊙O,與邊AC交于點M.
,點O是邊AB上的一個動點,以點O為圓心,OA為半徑作⊙O,與邊AC交于點M.
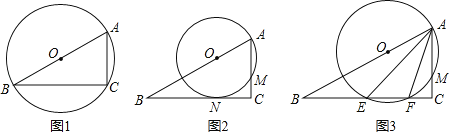
(1)如圖1,當(dāng)⊙O經(jīng)過點C時,⊙O的直徑是 ;
(2)如圖2,當(dāng)⊙O與邊BC相切時,切點為點N,試求⊙O與△ABC重合部分的面積;
(3)如圖3,當(dāng)⊙O與邊BC相交時,交點為E、F,設(shè)CM=x,就判斷AEAF是否為定值,若是,求出這個定值;若不是,請用含x的代數(shù)式表示.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
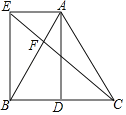
【題目】如圖,在△ABC中,AB=AC,D為BC中點,AE∥BD,且AE=BD.
(1)求證:四邊形AEBD是矩形;
(2)連接CE交AB于點F,若∠ABE=30°,AE=2,求EF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
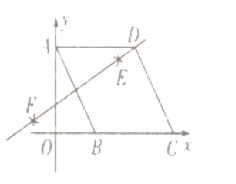
【題目】如圖,在菱形![]() 中,點
中,點![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() 分別以點
分別以點![]() 為圓心、大于
為圓心、大于![]() 的長為半徑作弧,兩弧相交于點
的長為半徑作弧,兩弧相交于點![]() .直線
.直線![]() 恰好經(jīng)過點
恰好經(jīng)過點![]() 則點
則點![]() 的坐標(biāo)為( )
的坐標(biāo)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小字計劃在某外賣網(wǎng)站點如下表所示的菜品,已知每份訂單的配送費為3元,商家為了促銷,對每份訂單的總價(不含配送費)提供滿減優(yōu)惠:滿30元減12元,滿60元減30元,滿100元減45元,如果小宇在購買下表中所有菜品時,采取適當(dāng)?shù)南掠唵畏绞剑敲此c餐的總費用最低可為___元.
菜品 | 單價(含包裝費) | 數(shù)量 |
| 30元 | 1 |
| 12元 | 1 |
| 30元 | 1 |
| 12元 | 1 |
| 3元 | 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】使用家用燃?xì)庠顭_同一壺水所需的燃?xì)饬?/span>![]() (單位:
(單位:![]() )與旋鈕的旋轉(zhuǎn)角度
)與旋鈕的旋轉(zhuǎn)角度![]() (單位:度)(
(單位:度)(![]() )近似滿足函數(shù)關(guān)系y=ax2+bx+c(a≠0).如圖記錄了某種家用燃?xì)庠顭_同一壺水的旋鈕角度
)近似滿足函數(shù)關(guān)系y=ax2+bx+c(a≠0).如圖記錄了某種家用燃?xì)庠顭_同一壺水的旋鈕角度![]() 與燃?xì)饬?/span>
與燃?xì)饬?/span>![]() 的三組數(shù)據(jù),根據(jù)上述函數(shù)模型和數(shù)據(jù),可推斷出此燃?xì)庠顭_一壺水最節(jié)省燃?xì)獾男o角度約為( )
的三組數(shù)據(jù),根據(jù)上述函數(shù)模型和數(shù)據(jù),可推斷出此燃?xì)庠顭_一壺水最節(jié)省燃?xì)獾男o角度約為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() ,以點
,以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑畫弧,與直線
的長為半徑畫弧,與直線![]() 位于第一象限的部分相交于點
位于第一象限的部分相交于點![]() ,則點
,則點![]() 的坐標(biāo)為_______.
的坐標(biāo)為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,反比例函數(shù)![]() (k是常數(shù),且
(k是常數(shù),且![]() )的圖象經(jīng)過點
)的圖象經(jīng)過點![]() .
.
(1)若b=4,求y關(guān)于x的函數(shù)表達(dá)式;
(2)點![]() 也在反比例函數(shù)y的圖象上:
也在反比例函數(shù)y的圖象上:
①當(dāng)![]() 且
且![]() 時,求b的取值范圍;
時,求b的取值范圍;
②若B在第二象限,求證:![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com