
【題目】如圖,在直角三角形ABC中,∠C=90°,AC=2,BC=2![]() ,點O是邊AB上的一個動點,以點O為圓心,OA為半徑作⊙O,與邊AC交于點M.
,點O是邊AB上的一個動點,以點O為圓心,OA為半徑作⊙O,與邊AC交于點M.
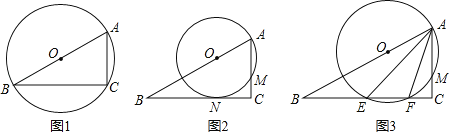
(1)如圖1,當⊙O經過點C時,⊙O的直徑是 ;
(2)如圖2,當⊙O與邊BC相切時,切點為點N,試求⊙O與△ABC重合部分的面積;
(3)如圖3,當⊙O與邊BC相交時,交點為E、F,設CM=x,就判斷AEAF是否為定值,若是,求出這個定值;若不是,請用含x的代數式表示.
【答案】(1)4;(2)![]() ;(3)不是定值,理由見解析
;(3)不是定值,理由見解析
【解析】
(1)由AB是圓的直徑知∠C=90°,再根據勾股定理求解可得;
(2)連結ON,OM,先證tan∠B=![]() 知∠B=30°,∠A=60°,∠BON=60°,∠AON=120°,設ON=OA=r,證△OBN∽△ABC得
知∠B=30°,∠A=60°,∠BON=60°,∠AON=120°,設ON=OA=r,證△OBN∽△ABC得![]() ,據此求出r的值,再計算出2S扇形MON和S△AOM,從而得出答案;
,據此求出r的值,再計算出2S扇形MON和S△AOM,從而得出答案;
(3)設⊙O與AB的另一交點為G,連結GE,OM,證△AGE∽△AFC得![]() ,由AC=2,CM=x知AM=2﹣x,再證∠AOM=60°得OA=AM=2﹣x,AG=2AO=4﹣2x,從而知AEAF=ACAG=8﹣4x,據此得出答案.
,由AC=2,CM=x知AM=2﹣x,再證∠AOM=60°得OA=AM=2﹣x,AG=2AO=4﹣2x,從而知AEAF=ACAG=8﹣4x,據此得出答案.
(1)∵AB是圓的直徑,
∴∠C=90°,
∵AC=2,BC=2![]() ,
,
∴AB=4故答案為4;
(2)如圖2,連結ON,OM,
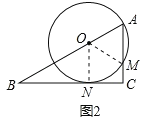
∵⊙O與邊BC相切于點N,
∴ON⊥BC
在Rt△ABC中,∠C=90°,AC=2,BC=2![]() ,
,
∴tan∠B=![]() ,
,
∴∠B=30°,∠A=60°,∠BON=60°,∠AON=120°,
∵OA=OM,
∴∠OMA=∠A=60°,
∴∠AOM=60°,∠MON=60°,
設ON=OA=r,
∵∠BNO=∠C=90°,∠B=∠B,
∴△OBN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得r=![]() ,
,
∴2S扇形MON=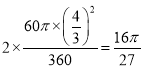 ,
,
∵S△AOM=![]() ,
,
∴⊙O與△ABC重合部分的面積是![]() .
.
(3)AEAF不為定值,理由如下:
如圖3,設⊙O與AB的另一交點為G,連結GE,OM,
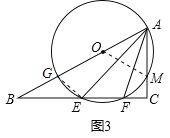
∵AG是⊙O的直徑,
∴∠GEA=90°=∠C,
在圓內接四邊形AGEF中,∠AGE+∠AFE=180°,
∵∠AFC+∠AFE=180°,
∴∠AGE=∠AFC,
∴△AGE∽△AFC,
∴![]() ,
,
∵AC=2,CM=x,
∴AM=2﹣x,
∵∠OMA=∠OAM=60°,
∴∠AOM=60°,
∴OA=AM=2﹣x,
AG=2AO=4﹣2x,
∴AEAF=ACAG=8﹣4x,
∵x不是定值
∴AEAF不是定值.


科目:初中數學 來源: 題型:
【題目】甲、乙兩人從少年宮出發,沿相同的路線分別以不同的速度勻速跑向體育館,甲先跑一段路程后,乙開始出發,當乙超出甲150米時,乙停在此地等候甲,兩人相遇后乙又繼續以原來的速度跑向體育館.如圖是甲、乙兩人在跑步的全過程中經過的路程y(米)與甲出發的時間x(秒)的函數圖象,則乙在途中等候甲用了( )秒
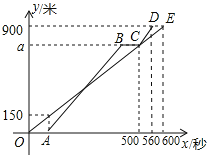
A.200B.150C.100D.80
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件![]() 元,出廠價為每件
元,出廠價為每件![]() 元,每月銷售量
元,每月銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間的關系近似滿足一次函數:
(元)之間的關系近似滿足一次函數:![]() .
.
(1)李明在開始創業的第一個月將銷售單價定為![]() 元,那么政府這個月為他承擔的總差價為多少元?
元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為![]() (元),當銷售單價定為多少元時,每月可獲得最大利潤?
(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于![]() 元.如果李明想要每月獲得的利潤不低于
元.如果李明想要每月獲得的利潤不低于![]() 元,那么政府為他承擔的總差價最少為多少元?
元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個批發店銷售同一種蘋果,在甲批發店,不論一次購買數量是多少,價格均為6元/![]() .在乙批發店,一次購買數量不超過
.在乙批發店,一次購買數量不超過![]() 時,價格為7元/
時,價格為7元/![]() ;一次購買數量超過
;一次購買數量超過![]() 時,其中有
時,其中有![]() 的價格仍為7元/
的價格仍為7元/![]() ,超過
,超過![]() 部分的價格為5元/
部分的價格為5元/![]() .設小王在同一個批發店一次購買蘋果的數量為
.設小王在同一個批發店一次購買蘋果的數量為![]() .
.
(Ⅰ)根據題意填空:
①若一次購買數量為![]() 時,在甲批發店的花費為________元,在乙批發店的花費為________元;
時,在甲批發店的花費為________元,在乙批發店的花費為________元;
②若一次購買數量為![]() 時,在甲批發店的花費為________元,在乙批發店的花費為________元;
時,在甲批發店的花費為________元,在乙批發店的花費為________元;
(Ⅱ)設在甲批發店花費![]() 元,在乙批發店花費
元,在乙批發店花費![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(Ⅲ)根據題意填空:
①若小王在甲批發店和在乙批發店一次購買蘋果的數量相同,且花費相同,則他在同一個批發店一次購買蘋果的數量為_________![]() ;
;
②若小王在同一個批發店一次購買蘋果的數量為![]() ,則他在甲、乙兩個批發店中的________批發店購買花費少;
,則他在甲、乙兩個批發店中的________批發店購買花費少;
③若小王在同一個批發店一次購買蘋果花費了260元,則他在甲、乙兩個批發店中的_________批發店購買數量多.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】桃花中學計劃購買![]() 兩種型號的小黑板,經洽談, 購買一塊
兩種型號的小黑板,經洽談, 購買一塊![]() 型小黑板比買一塊
型小黑板比買一塊![]() 型小黑板多
型小黑板多![]() 元,且購買
元,且購買![]() 塊
塊![]() 型小黑板和
型小黑板和![]() 塊
塊![]() 型小黑板共需
型小黑板共需![]() 元.
元.
(1)求購買一塊![]() 型小黑板和一塊
型小黑板和一塊![]() 型小黑板各需要多少元?
型小黑板各需要多少元?
(2)根據學校的實際情況,需購買![]() 兩種型號的小黑板共
兩種型號的小黑板共![]() 塊,并且購買
塊,并且購買![]() 型小黑板的數量不少于購買
型小黑板的數量不少于購買![]() 型小黑板的數量,請問學校購買這批小黑板最少要多少元?
型小黑板的數量,請問學校購買這批小黑板最少要多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,以
中,以![]() 為直徑的
為直徑的![]() 經過點
經過點![]() 過點
過點![]() 作
作![]() 的切線
的切線![]() 點
點![]() 是
是![]() 上不與點
上不與點![]() 重合的一個動點,連接
重合的一個動點,連接![]() .
.
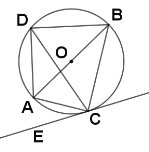
![]() 求證:
求證:![]() ;
;
![]() 填空:
填空:
![]() 當
當![]() _ 時,
_ 時,![]() 為等腰直角三角形:
為等腰直角三角形:
![]() 當
當![]() 時,四邊形
時,四邊形![]() 為菱形.
為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知m,n分別是關于x的一元二次方程ax2+bx+c=a與ax2+bx+c=b的一個根,且m=n+1.
(1)當m=2,a=﹣1時,求b與c的值;
(2)用只含字母a,n的代數式表示b;
(3)當a<0時,函數y=ax2+bx+c滿足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com