
【題目】已知:a、b為有理數,下列說法:①若 a、b互為相反數,則![]() ;②若
;②若![]() 則
則![]() ;③若
;③若![]() ,則
,則![]() ;④若
;④若![]() ,則
,則![]() 是正數.其中正確的有
是正數.其中正確的有
A.1個B.2個C.3個D.4個
【答案】B
【解析】
①0的相反數為0,而![]() 沒有意義;
沒有意義;
②由兩數之和小于0,兩數之積大于0,得到a與b都為負數,即3a+4b小于0,利用負數的絕對值等于它的相反數化簡得到結果,即可作出判斷;
③由ab的絕對值等于它的相反數,得到ab為非正數,得到a與b的大小,即可作出判斷;
④由a絕對值大于b絕對值,分情況討論,即可作出判斷.
①0與0互為相反數,但是![]() 沒有意義,本選項錯誤;
沒有意義,本選項錯誤;
②由a+b<0,ab>0,得到a與b同時為負數,即3a+4b<0,
∴|3a+4b|=3a4b,本選項正確;
③∵|ab|+ab=0,即|ab|=(ab),
∴ab≤0,即a≤b,本選項錯誤;
④若|a|>|b|,
當a>0,b>0時,可得a>b,即ab>0,a+b>0,∴(a+b)(ab)為正數;
當a>0,b<0時,ab>0,a+b>0,∴(a+b)(ab)為正數;
當a<0,b>0時,ab<0,a+b<0,∴(a+b)(ab)為正數;
當a<0,b<0時,ab<0,a+b<0,∴(a+b)(ab)為正數,
本選項正確,
則其中正確的有2個.
故選:B.
【點晴】
此題考查了有理數的混合運算,熟練掌握各種運算法則是解本題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解.并規定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)若F(a)=![]() 且a為100以內的正整數,則a=________;
且a為100以內的正整數,則a=________;
(2)如果m是一個兩位數,那么試問F(m)是否存在最大值或最小值?若存在,求出最大(或最小)值以及此時m的取值并簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖口袋中有5張完全相同的卡片,分別寫有![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,口袋外面有
,口袋外面有![]() 張卡片,分別寫有
張卡片,分別寫有![]() 和
和![]() .現隨機從口袋中取出一張卡片,與口袋外面的兩張卡片放在一起,以卡片上的數量分別作為三條線段的長度,回答下列問題:
.現隨機從口袋中取出一張卡片,與口袋外面的兩張卡片放在一起,以卡片上的數量分別作為三條線段的長度,回答下列問題:


(1)根據題目要求,寫出組合成的三條線度的長度的所有可能的結果;
(2)求這三條線段能組成三角形的概率;
(3)求這三條線段能組成等腰三角形的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知B,C,E三點在同一條直線上,△ABC與△DCE都是等邊三角形,其中線段BD交AC于點G,線段AE交CD于點F.求證:(1)△ACE≌△BCD;(2)![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
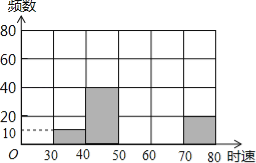
【題目】將某雷達測速區監測到的一組汽車的時速數據整理,得到其頻數分布表(未完成):
數據段 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 總計 |
頻 數 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注:30~40為時速大于等于30千米而小于40千米,其他類同.
(1)請你把表中的數據填寫完整;
(2)補全頻數分布直方圖;
(3)如果此路段汽車時速超過60千米即為違章,則違章車輛共有多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系內,已知點A(0,6),點B(8,0).動點P從A開始在線段AO上以每秒1個單位長度的速度向點O移動,同時動點Q從點B開始在線段BA上以每秒2個單位長度的速度向點A移動,設點P,Q移動的時間為t秒.
(1)求直線AB的解析式;
(2)當t為何值時,△APQ與△AOB相似,并求出此時點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
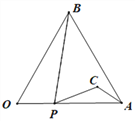
【題目】如圖,等邊△AOB的邊長為4,點P從點O出發,沿OA以每秒1個單位的速度向點A勻速運動,當點P到達點A時停止運動,設點P運動的時間是t秒.將線段BP的中點繞點P按順時針方向旋轉60°得點C,點C隨點P的運動而運動,連接CP、CA.在點P從O向A運動的過程中,當△PCA為直角三角形時t的值為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
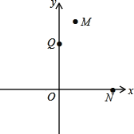
【題目】已知,在平面直角坐標系中,點M、N的坐標分別為(1,4)和(3,0),點Q是y軸上的一個動點,且M、N、Q三點不在同一直線上,當△MNQ的周長最小時,則點Q的坐標是___.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com