
【題目】一輛快車從甲地開往乙地,一輛慢車從乙地開往甲地,兩車同時出發(fā),設慢車離乙地為y1(km),快車離乙地的距離為y2(km),慢車行駛時間為x(h),兩車之間的距離為s(km),y1 ,y2與x的函數(shù)關系圖像如圖①所示,s與x的函數(shù)關系圖如圖②所示:

圖① 圖②
(1)圖中的a= ,b= .
(2)求s關于x的函數(shù)關系式.
(3)甲、乙兩地間有E、F兩個加油站,相距200km,若慢車進入加油站E時,快車恰好進入加油站F,請直接寫出加油站E到甲地的距離.
【答案】(1)6; ![]() ;(2)
;(2)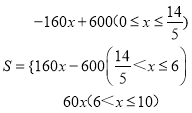 ;(3)加油站E到甲地的距離為300千米或450千米.
;(3)加油站E到甲地的距離為300千米或450千米.
【解析】(1)根據(jù)S與x之間的函數(shù)關系式可以得到當位于C點時,兩車之間的距離增加變緩,此時快車到站,指出此時a的值即可,求得a的值后求出兩車相遇時的時間即為b的值;
(2)根據(jù)函數(shù)的圖象可以得到A、B、C、D的點的坐標,利用待定系數(shù)法求得函數(shù)的解析式即可.
(3)分兩車相遇前和兩車相遇后兩種情況討論,當相遇前令s=200代入直線AB解析式,當相遇后令s=200代入直線BC解析式即可求得x的值.
解:(1)由S與x之間的函數(shù)的圖象可知:當位于C點時,兩車之間的距離增加變緩,
∴由此可以得到a=6,
∴快車每小時行駛100千米,慢車每小時行駛60千米,兩地之間的距離為600,
∴b=600÷(100+60)= ![]() ;
;
(2)∵從函數(shù)的圖象上可以得到A、B、C、D點的坐標分別為:(0,600)、(![]() ,0)、(6,360)、(10,600),
,0)、(6,360)、(10,600),
∴設線段AB所在直線解析式為:S=kx+b,
∴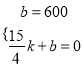 ,
,
解得:k=160,b=600,
設線段BC所在的直線的解析式為:S=kx+b,
∴
解得:k=160,b=600,
設直線CD的解析式為:S=kx+b,
∴![]() ,
,
解得:k=60,b=0
∴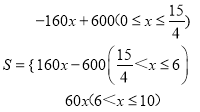 ;
;
(3)當兩車相遇前分別進入兩個不同的加油站,
此時:S=160x+600=200,
解得:x=![]() ,
,
當兩車相遇后分別進入兩個不同的加油站,
此時:S=160x600=200,
解得:x=5,
∴當x=![]() 或5時,此時E加油站到甲地的距離為450km或300km.
或5時,此時E加油站到甲地的距離為450km或300km.


科目:初中數(shù)學 來源: 題型:
【題目】小張騎自行車勻速從甲地到乙地,在途中休息了一段時間后,仍按原速行駛.他距乙地的距離y(km)與時間x(h)的關系如圖中折線所示,小李開車勻速從乙地到甲地,比小張晚出發(fā)一段時間,他距乙地的距離y(km)與時間x(h)的關系如圖中線段AB所示.
(1)小李到達甲地后,再經(jīng)過_______小時小張也到達乙地;小張騎自行車的速度是_______千米/小時.
(2)小張出發(fā)幾小時與小李相距15千米?
(3)若小李想在小張休息期間與他相遇,則他出發(fā)的時間x應在什么范圍?(直接寫出答案)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知A,D,E三點共線,C,B,F三點共線,AB=CD,AD=CB,DE=BF,那么BE與DF之間有什么數(shù)量關系?請說明理由.
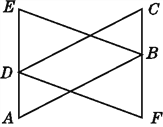
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AC是平行四邊形ABCD的對角線,∠BAC=∠DAC.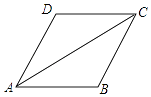
(1)求證:AB=BC;
(2)若AB=4,AC=4 ![]() ,求平行四邊形ABCD的面積.
,求平行四邊形ABCD的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列事件,是必然事件的是( )
A.投擲一次骰子向上一面的點數(shù)是6B.童威在罰球線上投籃一次未投中
C.任意畫一個多邊形其外角和是360°D.經(jīng)過有交通信號燈的路口遇到紅燈
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我們把分子為1的分數(shù)叫做單位分數(shù),如 ![]() ,
, ![]() ,
, ![]() ,…任何一個單位分數(shù)都可以拆分成兩個不同的單位分數(shù)的和,如
,…任何一個單位分數(shù)都可以拆分成兩個不同的單位分數(shù)的和,如 ![]() =
= ![]() +
+ ![]() ,
, ![]() =
= ![]() +
+ ![]() ,
, ![]() =
= ![]() +
+ ![]() ,…
,…
(1)根據(jù)對上述式子的觀察,你會發(fā)現(xiàn) ![]() =
= ![]() +
+ ![]() ,則a= , b=;
,則a= , b=;
(2)進一步思考,單位分數(shù) ![]() =
= ![]() +
+ ![]() (n是不小于2的正整數(shù)),則x=(用n的代數(shù)式表示)
(n是不小于2的正整數(shù)),則x=(用n的代數(shù)式表示)
(3)計算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下結論:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正確的有( ).
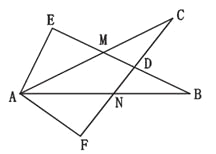
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,射線OA⊥射線OB,半徑![]() 的動圓M與OB相切于點Q,( 圓M 與OA沒有公共點 ), P是OA上的動點,且PM
的動圓M與OB相切于點Q,( 圓M 與OA沒有公共點 ), P是OA上的動點,且PM![]() .設OP=
.設OP= ![]()
![]() ,OQ=
,OQ= ![]()
![]() .
.
(1)求![]() 、
、![]() 所滿足的關系式,并寫出
所滿足的關系式,并寫出![]() 的取值范圍 ;
的取值范圍 ;
(2)當△MOP為等腰三角形時,求相應![]() 的值;
的值;
(3)是否存在大于2的實數(shù)![]() ,使△MQO∽△OMP?若存在,求相應
,使△MQO∽△OMP?若存在,求相應![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
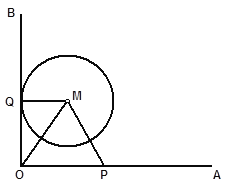
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com