
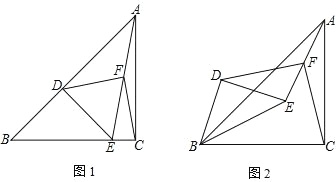
【題目】已知如圖 1,在△ABC 中,∠ACB=90°,BC=AC,點 D 在 AB 上,DE⊥AB交 BC 于 E,點 F 是 AE 的中點
(1) 寫出線段 FD 與線段 FC 的關系并證明;
(2) 如圖 2,將△BDE 繞點 B 逆時針旋轉α(0°<α<90°),其它條件不變,線段 FD 與線段 FC 的關系是否變化,寫出你的結論并證明;
(3) 將△BDE 繞點 B 逆時針旋轉一周,如果 BC=4,BE=2![]() ,直接寫出線段 BF 的范圍.
,直接寫出線段 BF 的范圍.
【答案】(1)結論:FD=FC,DF⊥CF;(2)結論不變.(3)![]() ≤BF≤3
≤BF≤3![]() .
.
【解析】
(1)根據直角三角形的性質先找出相關角、邊的關系,利用等量代換得到結果.(2)旋轉前后,圖形的性質是不變的,據此可以直接找到旋轉前后邊角的關系,從而證明結論(3)要使BF最長,只有點E落在AB上即可要使BF最短,只有點E落在AB的延長線即可.
(1)結論:FD=FC,DF⊥CF.
理由:如圖1中,
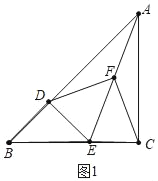
∵∠ADE=∠ACE=90°,AF=FE,
∴DF=AF=EF=CF,
∴∠FAD=∠FDA,∠FAC=∠FCA,
∴∠DFE=∠FDA+∠FAD=2∠FAD,∠EFC=∠FAC+∠FCA=2∠FAC,
∵CA=CB,∠ACB=90°,
∴∠BAC=45°,
∴∠DFC=∠EFD+∠EFC=2(∠FAD+∠FAC)=90°,
∴DF=FC,DF⊥FC.
(2)結論不變.
理由:如圖2中,延長AC到M使得CM=CA,延長ED到N,使得DN=DE,連接BN、BM.EM、AN,延長ME交AN于H,交AB于O.
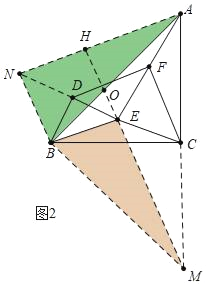
∵BC⊥AM,AC=CM,
∴BA=BM,同法BE=BN,
∵∠ABM=∠EBN=90°,
∴∠NBA=∠EBM,
∴△ABN≌△MBE,
∴AN=EM,∴∠BAN=∠BME,
∵AF=FE,AC=CM,
∴CF=![]() EM,FC∥EM,同法FD=
EM,FC∥EM,同法FD=![]() AN,FD∥AN,
AN,FD∥AN,
∴FD=FC,
∵∠BME+∠BOM=90°,∠BOM=∠AOH,
∴∠BAN+∠AOH=90°,
∴∠AHO=90°,
∴AN⊥MH,FD⊥FC.
(3)如圖3中,當點E落在AB上時,BF的長最大,最大值=3![]()
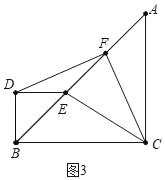
如圖4中,當點E落在AB的延長線上時,BF的值最小,最小值=![]() .
.
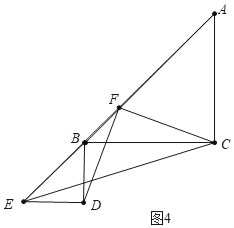
綜上所述,![]() ≤BF≤3
≤BF≤3![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,已知一次函數(shù)![]() (k≠0)的圖象與x軸、y軸分別交于A、B兩點,且與反比例函數(shù)
(k≠0)的圖象與x軸、y軸分別交于A、B兩點,且與反比例函數(shù)![]() (m≠0)的圖象在第一象限交于C點,CD垂直于x軸,垂足為D.若OA=OB=OD=1.
(m≠0)的圖象在第一象限交于C點,CD垂直于x軸,垂足為D.若OA=OB=OD=1.

(1)求點A、B、D的坐標;
(2)求一次函數(shù)和反比例函數(shù)的解析式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,∠B=90°,AB=12,BC=24,動點P從點A開始沿邊AB向終點B以每秒2個單位長度的速度移動,動點Q從點B開始沿邊BC以每秒4個單位長度的速度向終點C移動,如果點P、Q分別從點A、B同時出發(fā),那么△PBQ的面積S隨出發(fā)時間t(s)如何變化?寫出函數(shù)關系式及t的取值范圍.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在斜坡的頂部有一鐵塔AB,B是CD的中點,CD是水平的,在陽光的照射下,塔影DE留在坡面上.已知鐵塔底座寬CD=12 m,塔影長DE=18 m,小明和小華的身高都是1.6m,同一時刻,小明站在點E處,影子在坡面上,小華站在平地上,影子也在平地上,兩人的影長分別為2m和1m,那么塔高AB為( )
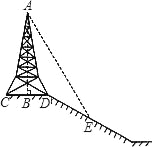
A. 24m B. 22m C. 20m D. 18m
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
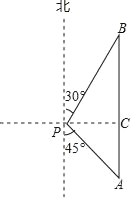
【題目】隨著航母編隊的成立,我國海軍日益強大,2018年4月12日,中央軍委在南海海域降重舉行海上閱兵,在閱兵之前我軍加強了海上巡邏,如圖,我軍巡邏艦在某海域航行到A處時,該艦在觀測點P的南偏東45°的方向上,且與觀測點P的距離PA為400海里;巡邏艦繼續(xù)沿正北方向航行一段時間后,到達位于觀測點P的北偏東30°方向上的B處,問此時巡邏艦與觀測點P的距離PB為多少海里?(參考數(shù)據:![]() ≈1.414,
≈1.414,![]() ≈1.732,結果精確到1海里).
≈1.732,結果精確到1海里).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】二次函數(shù)y=x2+(a﹣2)x+3的圖象與一次函數(shù)y=x(1≤x≤2)的圖象有且僅有一個交點,則實數(shù)a的取值范圍是( )
A. a=3±2![]() B. ﹣1≤a<2
B. ﹣1≤a<2
C. a=3![]() 或﹣
或﹣![]() ≤a<2 D. a=3﹣2
≤a<2 D. a=3﹣2![]() 或﹣1≤a<﹣
或﹣1≤a<﹣![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為提升學生的藝術素養(yǎng),學校計劃開設四門藝術選修課:A.書法;B.繪畫;C.樂器;D.舞蹈.為了解學生對四門功課的喜歡情況,在全校范圍內隨機抽取若干名學生進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中一門).將數(shù)據進行整理,并繪制成如下兩幅不完整的統(tǒng)計圖,請結合圖中所給信息解答下列問題:
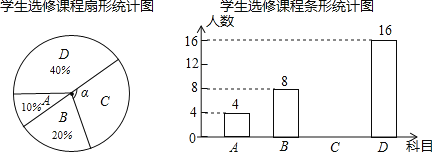
(1)本次調查的學生共有多少人?扇形統(tǒng)計圖中∠α的度數(shù)是多少?
(2)請把條形統(tǒng)計圖補充完整;
(3)學校為舉辦2018年度校園文化藝術節(jié),決定從A.書法;B.繪畫;C.樂器;D.舞蹈四項藝術形式中選擇其中兩項組成一個新的節(jié)目形式,請用列表法或樹狀圖求出選中書法與樂器組合在一起的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,甲樓樓高![]() 米,乙樓座落在甲樓的正北面,已知當?shù)囟林形?/span>
米,乙樓座落在甲樓的正北面,已知當?shù)囟林形?/span>![]() 時太陽光線與水平面的夾角為
時太陽光線與水平面的夾角為![]() ,此時求:
,此時求:
①如果兩樓相距![]() 米,那么甲樓的影子落在乙樓上有多高?________
米,那么甲樓的影子落在乙樓上有多高?________
②如果甲樓的影子剛好不落在乙樓上,那么兩樓的距離應當是________米.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com