
【題目】如圖,△ABC中,AB=AC,tanB=![]() , BC=4,E為BA延長線上一點,⊙E過點C與射線BC的另一交點為F,射線EF與射線AC交于P
, BC=4,E為BA延長線上一點,⊙E過點C與射線BC的另一交點為F,射線EF與射線AC交于P
(1)求證:AE2=AP·AC
(2)當F點在線段BC上時,設CF=x,△PFC的面積為y,求y與x的函數關系式并寫出x的取值范圍
(3)當![]() 時求BE
時求BE

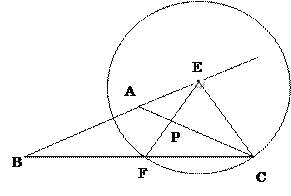
備用圖
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】分析:![]() 證明△AEP∽△ACE,根據相似三角形的性質得到
證明△AEP∽△ACE,根據相似三角形的性質得到![]() ,即可證明.
,即可證明.
![]() 證明△ECB∽△PFC.得到
證明△ECB∽△PFC.得到![]() ,求出
,求出![]() ,即可得到y與x的函數關系式.
,即可得到y與x的函數關系式.
![]() 分①
分①![]() ②
②![]() 兩種情況進行討論.
兩種情況進行討論.
詳解:(1)∵![]() ∴∠B=∠ACB
∴∠B=∠ACB
∵![]() ∴∠EFC=∠ECF
∴∠EFC=∠ECF
∵![]()
又∵![]()
∴∠BEF=∠ACE
∵![]()
∴△AEP∽△ACE.
∴![]() ∴
∴![]()
(2)∵∠B=∠ACB,∠ECF=∠EFC,
∴△ECB∽△PFC.
∴![]()
![]()
∵![]()
∴![]() .∴
.∴![]()
在Rt△BEH中,∵![]() ∴
∴![]() .
.
∴![]()
∴![]() .
.
∴![]()
(3) ①![]()
∵![]()
∴![]()
∵△AEP∽△ACE.
∴![]()
∴![]()
![]() .
.
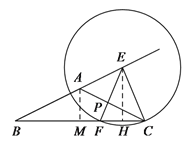
∵![]()
![]() ∴
∴![]()
在Rt△ABM中,∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
②![]()
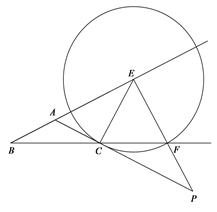
∵∠EFC=∠ECF,![]()
![]() .
.
又∵![]() ∴∠B =∠FCP.
∴∠B =∠FCP.
∴∠P =∠BEC.
∵![]()
∴△AEP∽△ACE,∴![]()
∵![]() ∴
∴![]()
∴![]()
∴![]() .
.
綜上所述,![]() 或
或![]() .
.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點O與平面直角坐標系的原點重合,點A,C分別在x軸,y軸上,點B的坐標為(-5,4),點D為邊BC上一點,連接OD,若線段OD繞點D順時針旋轉90°后,點O恰好落在AB邊上的點E處,則點E的坐標為( )

A. (-5,3) B. (-5,4) C. (-5,![]() ) D. (-5,2)
) D. (-5,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,要測量一個沼澤水潭的寬度.現由于不能直接測量,小軍是這樣操作的:他在平地上選取一點C,該點可以直接到達A與B點,接著他量出AC和BC的距離,并找出AC與BC的中點E、F,連接EF,測量EF的長,于是他便知道了水潭AB的長等于2EF,小軍的做法有道理嗎?說明理由.你還有比小軍更簡單的方法嗎?
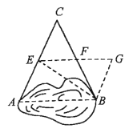
查看答案和解析>>
科目:初中數學 來源: 題型:
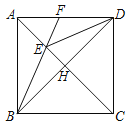
【題目】已知:如圖,邊長為1的正方形ABCD中,AC 、DB交于點H.DE平分∠ADB,交AC于點E.聯結BE并延長,交邊AD于點F.
(1)求證:DC=EC;
(2)求△EAF的面積.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了倡導節約能源,自某日起,我國對居民用電采用階梯電價,為了使大多數家庭不增加電費支出,事前就需要了解居民全年月平均用電量的分布情況,制訂一個合理的方案.某調查人員隨機調查了![]() 市
市![]() 戶居民全年月平均用電量(單位:千瓦時)數據如下:
戶居民全年月平均用電量(單位:千瓦時)數據如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下頻數分布表:
全年月平均用電量/千時 | 頻數 | 頻率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合計 |
|
|
畫出頻數分布直方圖,如下:

(1)補全數分布表和率分布直方圖
(2)若是根據數分布表制成扇形統計圖,則不低于![]() 千瓦時的部分圓心角的度數為_____________;
千瓦時的部分圓心角的度數為_____________;
(3)若![]() 市的階梯電價方案如表所示,你認為這個階梯電價方案合理嗎?
市的階梯電價方案如表所示,你認為這個階梯電價方案合理嗎?
檔次 | 全年月平均用電量/千瓦時 | 電價(元/千瓦時) |
第一檔 |
|
|
第二檔 |
|
|
第三檔 | 大于 |
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,
兩點,![]() 是
是![]() 的中點,
的中點,![]() 是線段
是線段![]() 上一點.
上一點.
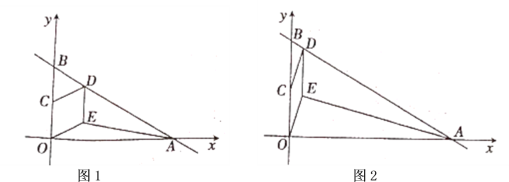
(1)求點![]() 、
、![]() 的坐標;
的坐標;
(2)若四邊形![]() 是菱形,如圖1,求
是菱形,如圖1,求![]() 的面積;
的面積;
(3)若四邊形![]() 是平行四邊形,如圖2,設點
是平行四邊形,如圖2,設點![]() 的橫坐標為
的橫坐標為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式.
的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明同學解方程的過程,請仔細閱讀,并解答所提出的問題.
![]()
解:去分母,得![]() ,①
,①
去括號,得![]() ,②
,②
移項,得![]() ,③
,③
合并同類項,得![]() ,④
,④
系數化為![]() ,得
,得![]() .⑤
.⑤
(1)聰明的你知道小明的解答過程在________(填序號)處出現了錯誤,出現錯誤的原因是違背了__________.
A.等式的基本性質![]() ;B.等式的基本性質
;B.等式的基本性質![]() ;C.去括號法則;D加法交換律.
;C.去括號法則;D加法交換律.
(2)請你寫出正確的解答過程
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)化簡求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=![]() .
.
(2)解答:老師在黑板上書寫了一個正確的演算過程,隨后用手掌捂住了一個多項式,形式如下:![]() +(-3x2+5x-7)=-2x2+3x-6.求所捂的多項式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多項式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com