
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,拋物線的對稱軸
點,拋物線的對稱軸![]() 與
與![]() 軸交于
軸交于![]() 點.
點.
(1)求拋物線的函數解析式;
(2)設點![]() 是直線
是直線![]() 上的一個動點,當
上的一個動點,當![]() 的值最小時,求
的值最小時,求![]() 的長;
的長;
(3)在直線![]() 上是否存在點
上是否存在點![]() ,使以
,使以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
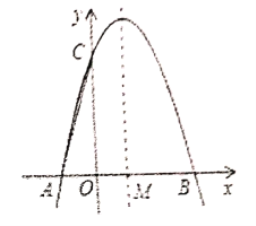
【答案】(1)![]() (2)
(2)![]() (3)存在,點
(3)存在,點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() 或
或![]() ,理由見解析
,理由見解析
【解析】
(1)由題意先求得C(0,3).設拋物線的解析式為y=a(x+1)(x-3),將點C的坐標代入可求得a的值即可;
(2)由題意依據軸對稱圖形的性質可知PA=PB,則PA+PC=PB+PC,則當點P在線段BC上時,PC+AP有最小值,PA+PC的最小值=BC,接下來,依據勾股定理求解即可;
(3)根據題意設點Q的坐標為(1,m),則QM=|m|,然后依據相似三角形的性質可得到∠OQM=∠CAO或∠OQM=∠ACO,然后依據相似三角形的性質列比例求解即可.
解:(1)把![]() 代入拋物線
代入拋物線![]() 中,得
中,得![]()
![]()
設拋物線的解析式為![]()
將點![]() 的坐標代入,得
的坐標代入,得![]()
解得![]()
![]() 拋物線的解析式為
拋物線的解析式為![]() .
.
(2)如圖所示:
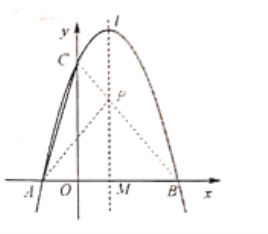
![]() 點
點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,點
對稱,點![]() 在直線
在直線![]() 上
上
![]()
![]()
![]() 兩點之間線段最短
兩點之間線段最短
![]() 當點
當點![]() 在線段
在線段![]() 上時,
上時,![]() 有最小值,
有最小值,
![]() 的最小值即為
的最小值即為![]()
![]() ,
,![]()
![]()
![]() 的最小值為
的最小值為![]() .
.
(3)拋物線的對稱軸為直線![]()
設點![]() 的坐標為
的坐標為![]() ,則
,則![]()
![]() 以
以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,
相似,
![]() 或
或![]()
當![]() 時,
時,![]()
即![]() ,解得
,解得![]()
![]() 點
點![]() 的坐標為
的坐標為![]() 或
或![]()
當![]() 時,
時,![]()
即![]() ,解得
,解得![]()
![]() 點
點![]() 的坐標為
的坐標為![]() 或
或![]()
綜上所述,點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB如圖,
(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作弧DE,交射線OB于點F,連接CF;
(2)以點F為圓心,CF長為半徑作弧,交弧DE于點G;
(3)連接FG,CG.作射線OG.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
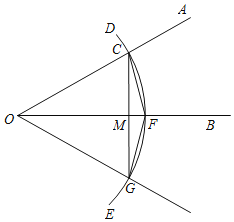
A.∠BOG=∠AOBB.若CG=OC,則∠AOB=30°
C.OF垂直平分CGD.CG=2FG
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與一次函數
與一次函數![]() 的圖象交于點
的圖象交于點![]() 與反比例函數
與反比例函數![]() 的圖象交于點
的圖象交于點![]() ,點
,點![]() 與點
與點![]() 關于
關于![]() 軸對稱.
軸對稱.
(1)直接寫出點![]() 的坐標;
的坐標;
(2)求點![]() 的坐標(用含
的坐標(用含![]() 的式子表示);
的式子表示);
(3)若![]() 兩點中只有一個點在線段
兩點中只有一個點在線段![]() 上,直接寫出
上,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
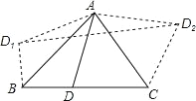
【題目】如圖,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC邊上異于點B,C的一動點,將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
+2,D是BC邊上異于點B,C的一動點,將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點C、D在線段AB上,若點C是線段AD的中點,2BD>AD,則下列結論正確的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】疫情無情人有情,愛心捐款傳真情.新冠肺炎疫情發生后,某班學生積極參加獻愛心活動,該班![]() 名學生的捐款統計情況如下表,關于捐款金額,下列說法錯誤的是( )
名學生的捐款統計情況如下表,關于捐款金額,下列說法錯誤的是( )
金額/元 | 10 | 20 | 30 | 50 | 100 |
人數 | 2 | 18 | 10 | 8 | 2 |
A.平均數為![]() 元B.眾數為
元B.眾數為![]() 元C.中位數為
元C.中位數為![]() 元D.極差為
元D.極差為![]() 元
元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第24屆冬奧會將于2022年在北京和張家口舉行,冬奧會的項目有滑雪(如高山滑雪、單板滑雪等),滑冰(如速度滑冰、花樣滑冰等),冰球,冰壺等.如圖,有4張形狀、大小、質地均相同的卡片,正面分別印有單板滑雪、速度滑冰、冰球、冰壺4種不同的圖案,背面完全相同.現將這4張卡片洗勻后正面向下放在桌子上.

(1)從中隨機抽取1張,抽出的卡片上恰好是滑雪項目圖案的概率是 .
(2)若印有單板滑雪、速度滑冰、冰球、冰壺4種不同圖案的卡片分別用A,B,C,D表示,從中隨機抽取兩張,試用畫樹狀圖或列表的方法求出印有冰球圖案的卡片被抽中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com