
【題目】2019年春節,小娜家購買了4個燈籠,燈籠上分別寫有“歡”、“度”、“春”、“節”(外觀完全一樣).
(1)小娜抽到“2019年”是 事件,“歡”字被抽中的是 事件;(填“不可能”或“必然”或“隨機”).小娜從四個燈籠中任取一個,取到“春”的概率是 .
(2)小娜從四個燈籠中先后取出兩個燈籠,請用列表法或畫樹狀圖法求小娜恰好取到“春”、“節”兩個燈籠的概率.
 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
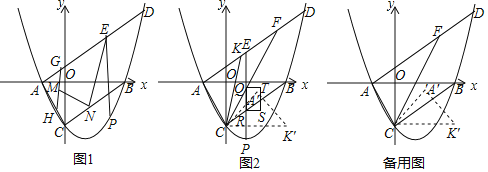
【題目】如圖,拋物線y=![]() 與x軸交于A,B(點A在點B的左側)與y軸交于點C,連接AC、BC.過點A作AD∥BC交拋物線于點D(8
與x軸交于A,B(點A在點B的左側)與y軸交于點C,連接AC、BC.過點A作AD∥BC交拋物線于點D(8![]() ,10),點P為線段BC下方拋物線上的任意一點,過點P作PE∥y軸交線段AD于點E.
,10),點P為線段BC下方拋物線上的任意一點,過點P作PE∥y軸交線段AD于點E.
(1)如圖1.當PE+AE最大時,分別取線段AE,AC上動點G,H,使GH=5,若點M為GH的中點,點N為線段CB上一動點,連接EN、MN,求EN+MN的最小值;
(2)如圖2,點F在線段AD上,且AF:DF=7:3,連接CF,點Q,R分別是PE與線段CF,BC的交點,以RQ為邊,在RQ的右側作矩形RQTS,其中RS=2,作∠ACB的角平分線CK交AD于點K,將△ACK繞點C順時針旋轉75°得到△A′CK′,當矩形RQTS與△A′CK′重疊部分(面積不為0)為軸對稱圖形時,請直接寫出點P橫坐標的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
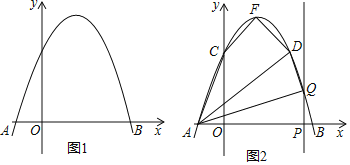
【題目】如圖1,拋物線y=ax2+bx+3交x軸于點A(﹣1,0)和點B(3,0).
(1)求該拋物線所對應的函數解析式;
(2)如圖2,該拋物線與y軸交于點C,頂點為F,點D(2,3)在該拋物線上.
①求四邊形ACFD的面積;
②點P是線段AB上的動點(點P不與點A、B重合),過點P作PQ⊥x軸交該拋物線于點Q,連接AQ、DQ,當△AQD是直角三角形時,求出所有滿足條件的點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
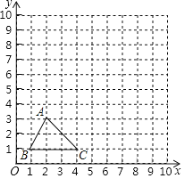
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點三角形![]() 頂點是網格線的交點
頂點是網格線的交點![]()
![]() 先將
先將![]() 豎直向上平移3個單位,再水平向右平移5個單位得到
豎直向上平移3個單位,再水平向右平移5個單位得到![]() ,請畫出
,請畫出![]() ;
;
![]() 將
將![]() 繞
繞![]() 點順時針旋轉
點順時針旋轉![]() ,得
,得![]() ,請畫出
,請畫出![]() ;
;
![]() 線段
線段![]() 變換到
變換到![]() 的過程中掃過區域的面積為______;
的過程中掃過區域的面積為______;
![]() 經過A、C兩點的函數解析式為______.
經過A、C兩點的函數解析式為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】魏晉時期的數學家劉徽首創割圓術.為計算圓周率建立了嚴密的理論和完善的算法.作圓內接正多邊形,當正多邊形的邊數不斷增加時,其周長就無限接近圓的周長,進而可用![]() 來求得較為精確的圓周率.祖沖之在劉徽的基礎上繼續努力,當正多邊形的邊數增加24576時,得到了精確到小數點后七位的圓周率,這一成就在當時是領先其他國家一千多年,如圖,依據“割圓術”,由圓內接正六邊形算得的圓周率的近似值是( )
來求得較為精確的圓周率.祖沖之在劉徽的基礎上繼續努力,當正多邊形的邊數增加24576時,得到了精確到小數點后七位的圓周率,這一成就在當時是領先其他國家一千多年,如圖,依據“割圓術”,由圓內接正六邊形算得的圓周率的近似值是( )
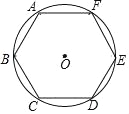
A. 0.5B. 1C. 3D. π
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,![]() ,連結AC,過點C作直線l∥AB,點P是直線l上的一個動點,直線PA與⊙O交于另一點D,連結CD,設直線PB與直線AC交于點E.
,連結AC,過點C作直線l∥AB,點P是直線l上的一個動點,直線PA與⊙O交于另一點D,連結CD,設直線PB與直線AC交于點E.
(1)求∠BAC的度數;
(2)當點D在AB上方,且CD⊥BP時,求證:PC=AC;
(3)在點P的運動過程中
①當點A在線段PB的中垂線上或點B在線段PA的中垂線上時,求出所有滿足條件的∠ACD的度數;
②設⊙O的半徑為6,點E到直線l的距離為3,連結BD,DE,直接寫出△BDE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場準備進一批兩種不同型號的衣服,已知購進A種型號衣服9件,B種型號衣服10件,則共需1810元;若購進A種型號衣服12件,B種型號衣服8件,共需1880元;已知銷售一件A型號衣服可獲利18元,銷售一件B型號衣服可獲利30元,要使在這次銷售中獲利不少于699元,且A型號衣服不多于28件.
(1)求A、B型號衣服進價各是多少元?
(2)若已知購進A型號衣服是B型號衣服的2倍還多4件,則商店在這次進貨中可有幾種方案并簡述購貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件50元.當售價為每件70元時,每星期可賣出300件,現需降價處理,且經市場調查:每降價1元,每星期可多賣出20件.在確保盈利的前提下,解答下列問題:
(1)若設每件降價x元、每星期售出商品的利潤為y元,請寫出y與x的函數關系式,并求出自變量x的取值范圍;
(2)當降價多少元時,每星期的利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com