
【題目】已知橢圓![]() 中心在原點,焦點在
中心在原點,焦點在![]() 軸上,且其焦點和短軸端點都在圓
軸上,且其焦點和短軸端點都在圓![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)點![]() 是圓
是圓![]() 上一點,過點
上一點,過點![]() 作圓
作圓![]() 的切線交橢圓
的切線交橢圓![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)由題意設出橢圓的標準方程,由于橢圓焦點和短軸端點都在圓![]() :
:![]() 上,可得到
上,可得到![]() ,
,![]() 的值,即可求出橢圓方程。
的值,即可求出橢圓方程。
(2)分類討論切線方程斜率存在與不存在的情況,當斜率不存在時,可直接確定![]() 的值,再討論斜率存在時,設出直線方程與橢圓方程聯立,利用韋達定理表示出
的值,再討論斜率存在時,設出直線方程與橢圓方程聯立,利用韋達定理表示出![]() ,再結合直線與圓相切性質消去一個參數,利用函數的單調性確定
,再結合直線與圓相切性質消去一個參數,利用函數的單調性確定![]() 的范圍,最后得到
的范圍,最后得到![]() 的最大值。
的最大值。
(1)由橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,故設橢圓
軸上,故設橢圓![]() 的標準方程為
的標準方程為![]() ,
,
![]() 橢圓的右焦點坐標為
橢圓的右焦點坐標為![]() ,上頂點坐標為
,上頂點坐標為![]()
![]() 橢圓
橢圓![]() 焦點和短軸端點都在圓
焦點和短軸端點都在圓![]() :
:![]() 上,
上,
![]()
![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() ,
,
橢圓![]() 的標準方程為
的標準方程為![]()
(2)當切線![]() 的斜率不存在時,切線方程為:
的斜率不存在時,切線方程為:![]() ,與橢圓
,與橢圓![]() 的兩個交點為
的兩個交點為![]() 或
或![]() ,則
,則![]() ,
,
當切線![]() 的斜率存在時,設切線方程為:
的斜率存在時,設切線方程為:![]() ,切線與橢圓交點的坐標分別為
,切線與橢圓交點的坐標分別為![]() ,
,![]() ,
,
聯立方程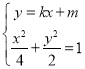 ,得:
,得:![]() ,
,
由于切線與橢圓相交于兩點,則![]() ,
,
由韋達定理可得: ,
,
又![]() 直線
直線![]() 與圓
與圓![]() 相切,
相切,
![]()
![]() ,即
,即![]() ,
,
![]()
![]()
![]()
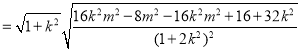




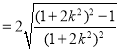
![]()
令![]() ,則函數
,則函數![]() 單調遞增,當
單調遞增,當![]() ,
,![]()
![]()
![]() ,
,
綜上所述,![]()


科目:高中數學 來源: 題型:
【題目】裝有除顏色外完全相同的6個白球、4個黑球和2個黃球的箱中隨機地取出兩個球,規定每取出1個黑球贏2元,而每取出1個白球輸1元,取出黃球無輸贏.
(1)以X表示贏得的錢數,隨機變量X可以取哪些值?求X的分布列;
(2)求出贏錢(即![]() 時)的概率.
時)的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列“若p,則q”形式的命題中,哪些命題中的q是p的必要條件?
(1)若四邊形為平行四邊形,則這個四邊形的兩組對角分別相等;
(2)若兩個三角形相似,則這兩個三角形的三邊成比例;
(3)若四邊形的對角線互相垂直,則這個四邊形是菱形;
(4)若![]() ,則
,則![]() ;
;
(5)若![]() ,則
,則![]() ;
;
(6)若![]() 為無理數,則x,y為無理數.
為無理數,則x,y為無理數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區農產品近幾年的產量統計如下表:

為了研究計算的方便,工作人員將上表的數據進行了處理,![]() 得到下表:
得到下表:

(1)根據表中數據,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)若近幾年該農產品每萬噸的價格![]() (萬元)與年產量
(萬元)與年產量![]() (萬噸)滿足
(萬噸)滿足![]() ,且每年該農產品都能售完,當年產量
,且每年該農產品都能售完,當年產量![]() 為何值時,銷售額
為何值時,銷售額![]() 最大?
最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: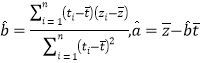 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三角形的三個頂點的坐標分別為![]() ,
,![]() ,
,![]() ,則該三角形的重心(三邊中線交點)的坐標為
,則該三角形的重心(三邊中線交點)的坐標為![]() .類比這個結論,連接四面體的一個頂點及其對面三角形重心的線段稱為四面體的中線,四面體的四條中線交于一點,該點稱為四面體的重心.若四面體的四個頂點的空間坐標分別為
.類比這個結論,連接四面體的一個頂點及其對面三角形重心的線段稱為四面體的中線,四面體的四條中線交于一點,該點稱為四面體的重心.若四面體的四個頂點的空間坐標分別為![]() ,
,![]() ,
,![]() ,
,![]() ,則該四面體的重心的坐標為( )
,則該四面體的重心的坐標為( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高一學年結束后,要對某班的50名學生進行文理分班,為了解數學對學生選擇文理科是否有影響,有人對該班的分科情況做了如下的數據統計:
理科人數 | 文科人數 | 總計 | |
數學成績好的人數 | 25 | 30 | |
數學成績差的人數 | 10 | ||
合計 | 15 |
(Ⅰ)根據數據關系,完成![]() 列聯表;
列聯表;
(Ⅱ)通過計算判斷能否在犯錯誤的概率不超過![]() 的前提下認為數學對學生選擇文理科有影響.
的前提下認為數學對學生選擇文理科有影響.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為4,動點E,F在棱
的棱長為4,動點E,F在棱![]() 上,動點P,Q分別在棱AD,CD上。若
上,動點P,Q分別在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),則四面體PEFQ的體積
大于零),則四面體PEFQ的體積
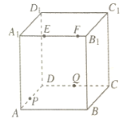
A.與![]() 都有關B.與m有關,與
都有關B.與m有關,與![]() 無關
無關
C.與p有關,與![]() 無關D.與π有關,與
無關D.與π有關,與![]() 無關
無關
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com