
題目列表(包括答案和解析)
補全證明過程
已知:如圖,∠1=∠2,∠C=∠D。
求證:∠A=∠F。

證明:∵∠1=∠2(已知),
又∠1=∠DMN(___________________),
∴∠2=∠_________(等量代換)。
∴DB∥EC(同位角相等,兩直線平行)。

∴∠A=∠F(兩直線平行,內錯角相等)。
完成下面推理過程:
如圖,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
證明 :∵∠1 =∠2(已知),且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代換).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B( ).
∴AB∥CD(________________________________).
(14分)在研究勾股定理時,同學們都見到過圖1,∠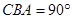 ,四邊形
,四邊形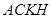 、
、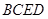 、
、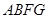 都是正方形.
都是正方形.
⑴連結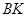 、
、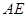 得到圖2,則△
得到圖2,則△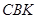 ≌△
≌△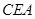 ,此時兩個三角形全等的判定依據是
,此時兩個三角形全等的判定依據是
▲ ;過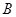 作
作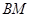 ⊥
⊥ 于
于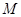 ,交
,交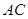 于
于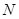 ,則
,則 △
△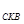 ;同理
;同理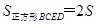 △
△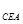 ,得
,得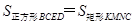 ,然后可證得勾股定理.
,然后可證得勾股定理.
⑵在圖1中,若將三個正方形“退化”為正三角形,得到圖3,同學們可以探究△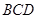 、△
、△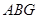 、△
、△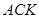 的面積關系是 ▲ .
的面積關系是 ▲ .
⑶為了研究問題的需要,將圖1中的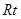 △
△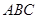 也進行“退化”為銳角△
也進行“退化”為銳角△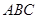 ,并擦去正方形
,并擦去正方形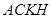 得圖4,由
得圖4,由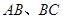 兩邊向三角形外作正△
兩邊向三角形外作正△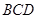 、正△
、正△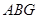 ,△
,△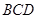 的外接圓與
的外接圓與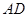 交于點
交于點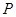 ,此時
,此時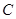 、
、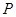 、
、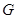 共線,從△
共線,從△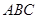 內一點到
內一點到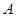 、
、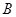 、
、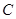 三個頂點的距離之和最小的點恰為點
三個頂點的距離之和最小的點恰為點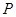 (已經被他人證明).設
(已經被他人證明).設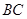 =3,
=3,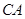 =4,
=4,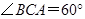 .求
.求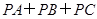 的值.
的值.
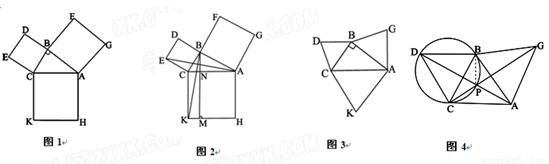
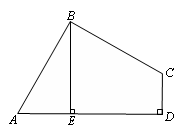
已知:如圖,在四邊形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求證:AB=BC;
(2)當BE⊥AD于E時,試證明:BE=AE+CD.
 ,四邊形
,四邊形 、
、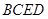 、
、 都是正方形.
都是正方形.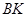 、
、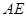 得到圖2,則△
得到圖2,則△ ≌△
≌△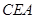 ,此時兩個三角形全等的判定依據是
,此時兩個三角形全等的判定依據是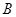 作
作 ⊥
⊥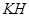 于
于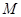 ,交
,交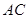 于
于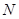 ,則
,則 △
△ ;同理
;同理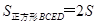 △
△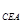 ,得
,得 ,然后可證得勾股定理.
,然后可證得勾股定理.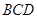 、△
、△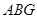 、△
、△ 的面積關系是 ▲ .
的面積關系是 ▲ .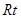 △
△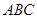 也進行“退化”為銳角△
也進行“退化”為銳角△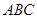 ,并擦去正方形
,并擦去正方形 得圖4,由
得圖4,由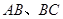 兩邊向三角形外作正△
兩邊向三角形外作正△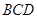 、正△
、正△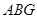 ,△
,△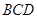 的外接圓與
的外接圓與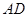 交于點
交于點 ,此時
,此時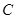 、
、 、
、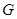 共線,從△
共線,從△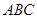 內一點到
內一點到 、
、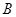 、
、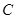 三個頂點的距離之和最小的點恰為點
三個頂點的距離之和最小的點恰為點 (已經被他人證明).設
(已經被他人證明).設 =3,
=3,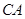 =4,
=4, .求
.求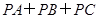 的值.
的值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com