
題目列表(包括答案和解析)
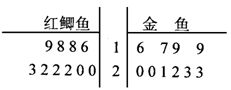
某觀賞魚池塘中養殖大量的紅鯽魚與金魚,為了估計池中兩種魚數量情況,養殖人員從池中捕出紅鯽魚和金魚各1000只,并給每只魚作上不影響其存活的記號,然后放回池內,經過一定時間后,再從池中隨機捕出1000只魚,分別記錄下其中有記號的魚數目,再放回池中,這樣的記錄作了10次,將記錄數據制成如右的莖葉圖。
(I)根據莖葉圖分別計算有記號的兩種魚的平均數,并估計池塘中兩種魚的數量。
(II)隨機從池塘中逐只有放回地捕出3只魚,求恰好是1只金魚2只紅鯽魚的概率。
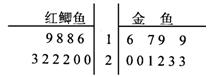 |
某觀賞魚池塘中養殖大量的紅鯽魚與金魚,為了估計池中兩種魚數量情況,養殖人員從池中捕出紅鯽魚和金魚各1000只,并給每只魚作上不影響其存活的記號,然后放回池內,經過一定時間后,再從池中隨機捕出1000只魚,分別記錄下其中有記號的魚數目,再放回池中,這樣的記錄作了10次,將記錄數據制成如右的莖葉圖。
(I)根據莖葉圖分別計算有記號的兩種魚的平均數,并估計池塘中兩種魚的數量。
(II)隨機從池塘中逐只有放回地捕出3只魚,求恰好是1只金魚2只紅鯽魚的概率。
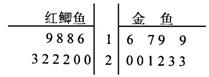 |
某觀賞魚池塘中養殖大量的紅鯽魚與金魚,為了估計池中兩種魚數量情況,養殖人員從池中捕出紅鯽魚和金魚各1000只,并給每只魚作上不影響其存活的記號,然后放回池內,經過一定時間后,再從池中隨機捕出1000只魚,分別記錄下其中有記號的魚數目,再放回池中,這樣的記錄作了10次,將記錄數據制成如右的莖葉圖。
(I)根據莖葉圖分別計算有記號的兩種魚的平均數,并估計池塘中兩種魚的數量。
(II)隨機從池塘中逐只有放回地捕出3只魚,求恰好是1只金魚2只紅鯽魚的概率。
 |
 已知某人工養殖觀賞魚池塘中養殖著大量的紅鯽魚與中國金魚.為了估計池塘中這兩種魚的數量,養殖人員從水庫中捕出了紅鯽魚與中國金魚各1000只,給每只魚作上不影響其存活的記號,然后放回池塘,經過一定時間,再每次從池塘中隨機地捕出1000只魚,分類記錄下其中有記號的魚的數目,隨即將它們放回池塘中.這樣的記錄作了10次,將記錄獲取的數據作成如圖的莖葉圖.
已知某人工養殖觀賞魚池塘中養殖著大量的紅鯽魚與中國金魚.為了估計池塘中這兩種魚的數量,養殖人員從水庫中捕出了紅鯽魚與中國金魚各1000只,給每只魚作上不影響其存活的記號,然后放回池塘,經過一定時間,再每次從池塘中隨機地捕出1000只魚,分類記錄下其中有記號的魚的數目,隨即將它們放回池塘中.這樣的記錄作了10次,將記錄獲取的數據作成如圖的莖葉圖.
一.選擇題 1-5 6-10 11-12 BCDCA DADBC AC
二.填空題 13.  ; 14.
; 14.  ;
15.
;
15.  ;
;
16. 
三、解答題
17.【解】(Ⅰ)由 整理得
整理得 ,
,
即 ,------2分
,------2分
∴ , -------5分
, -------5分
∵ ,∴
,∴ 。
-------7分
。
-------7分
【解】(Ⅱ)∵ ,∴最長邊為
,∴最長邊為 ,
--------8分
,
--------8分
∵
 ,∴
,∴ ,
--------10分
,
--------10分
∴ 為最小邊,由余弦定理得
為最小邊,由余弦定理得 ,解得
,解得 ,
,
∴ ,即最小邊長為1
--------12分
,即最小邊長為1
--------12分
18.【解】(Ⅰ)∵ ,∴
,∴ .---2分
.---2分
令 ,得
,得 ,
,
∵ ,∴
,∴ ,即
,即 ,∴
,∴ ,------4分
,------4分
當 時,
時, ,
, 的單調遞增區間為
的單調遞增區間為 ;------5分
;------5分
當 時,
時, .------6分
.------6分
 的單調遞減區間為
的單調遞減區間為 和
和 .------7分
.------7分
(Ⅱ)∵ 時,
時, ;------8分
;------8分
 時,
時, ;
; 時,
時, ,------9分
,------9分
∴ 處取得極大值-7. ------10分
處取得極大值-7. ------10分
即 ,解得
,解得 .------12分
.------12分
19.【解】(Ⅰ)由莖葉圖可求出10次記錄下的有記號的紅鯽魚與中國金魚數目的平均數均為20,故可認為池塘中的紅鯽魚與中國金魚的數目相同,設池塘中兩種魚的總數是 ,則有
,則有
 ,
------------3分
,
------------3分
即  ,
,
所以,可估計水庫中的紅鯽魚與中國金魚的數量均為25000. ------------6分
(Ⅱ)從上述對總體的估計數據獲知,從池塘隨機捕出1只魚,它是中國金魚的概率為 .隨機地從池塘逐只有放回地捕出5只魚,5只魚都是紅鯽魚的概率是
.隨機地從池塘逐只有放回地捕出5只魚,5只魚都是紅鯽魚的概率是 ,所以其中至少有一只中國金魚的概率
,所以其中至少有一只中國金魚的概率 .------12分
.------12分
20.【解】在 中,
中, ,
, ,∴
,∴ .
.
∵ ,∴四邊形
,∴四邊形 為正方形.
為正方形.
 ----6分
----6分
(Ⅱ)當點 為棱
為棱 的中點時,
的中點時, 平面
平面 .
------8分
.
------8分
 證明如下:
證明如下:
如圖,取 的中點
的中點 ,連
,連 、
、 、
、 ,
,
∵ 、
、 、
、 分別為
分別為 、
、 、
、 的中點,
的中點,
∴ .
.
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 . ------10分
. ------10分
同理可證 平面
平面 .
.
∵ ,
,
∴平面
 平面
平面 .
.
∵ 平面
平面 ,∴
,∴ 平面
平面 . ------12分
. ------12分
21.【解】(Ⅰ)法1:依題意顯然 的斜率存在,可設直線
的斜率存在,可設直線 的方程為
的方程為 ,
,
整理得  . ① ---------------------2分
. ① ---------------------2分
設 是方程①的兩個不同的根,
是方程①的兩個不同的根,
∴ , ②
----------------4分
, ②
----------------4分
且 ,由
,由 是線段
是線段 的中點,得
的中點,得
 ,∴
,∴ .
.
解得 ,這個值滿足②式,
,這個值滿足②式,
于是,直線 的方程為
的方程為 ,即
,即 --------------6分
--------------6分
法2:設 ,
, ,則有
,則有
 --------2分
--------2分
依題意, ,∴
,∴ .
---------------------4分
.
---------------------4分
∵ 是
是 的中點,
∴
的中點,
∴ ,
, ,從而
,從而 .
.
直線 的方程為
的方程為 ,即
,即 . ----------------6分
. ----------------6分
(Ⅱ)∵ 垂直平分
垂直平分 ,∴直線
,∴直線 的方程為
的方程為 ,即
,即 ,
,
代入橢圓方程,整理得 . ③
---------------8分
. ③
---------------8分
又設 ,
, 的中點為
的中點為 ,則
,則 是方程③的兩根,
是方程③的兩根,
∴ ,
, .-----10分
.-----10分
 到直線
到直線 的距離
的距離 ,故所求的以線段
,故所求的以線段 的中點
的中點 為圓心且與直線
為圓心且與直線 相切的圓的方程為:
相切的圓的方程為: .-----------12分
.-----------12分
22.【解】(Ⅰ)由 求導得
求導得 ,
,
∴曲線 :
: 在點
在點 處的切線方程為
處的切線方程為 ,即
,即 .
.
此切線與 軸的交點
軸的交點 的坐標為
的坐標為 ,
,
∴點 的坐標為
的坐標為 .即
.即 .
-------------------2分
.
-------------------2分
∵點 的坐標為
的坐標為 (
( ),
), 在曲線
在曲線 上,所以
上,所以 ,
,
∴曲線 :
: 在點
在點
 處的切線方程為
處的切線方程為 ---4分
---4分
令 ,得點
,得點 的橫坐標為
的橫坐標為 .
.
∴數列 是以2為首項,2為公比的等比數列.
是以2為首項,2為公比的等比數列.
∴ (
( ).
------------------6分
).
------------------6分
(Ⅱ)∵ ;
; ,
,


∴
 .---------10分
.---------10分
(Ⅲ)因為 ,所以
,所以 ,
,
所以數列 的前n項和
的前n項和 的前n項和為
的前n項和為 ①,
①,
---------12分

 ②,
②,
①―②得


 ,
,
所以 ---------14分
---------14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com