
題目列表(包括答案和解析)
設(shè)函數(shù) .
.
(I)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)當(dāng)0<a<2時,求函數(shù) 在區(qū)間
在區(qū)間 上的最小值.
上的最小值.
【解析】第一問定義域為真數(shù)大于零,得到 .
. .
.
令 ,則
,則 ,所以
,所以 或
或 ,得到結(jié)論。
,得到結(jié)論。
第二問中, (
( ).
).
 .
.
因為0<a<2,所以 ,
, .令
.令 可得
可得 .
.
對參數(shù)討論的得到最值。
所以函數(shù) 在
在 上為減函數(shù),在
上為減函數(shù),在 上為增函數(shù).
上為增函數(shù).
(I)定義域為 . ………………………1分
. ………………………1分
 .
.
令 ,則
,則 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因為定義域為 ,所以
,所以 .
.
令 ,則
,則 ,所以
,所以 .
.
因為定義域為 ,所以
,所以 . ………………………5分
. ………………………5分
所以函數(shù)的單調(diào)遞增區(qū)間為 ,
,
單調(diào)遞減區(qū)間為 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因為0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函數(shù) 在
在 上為減函數(shù),在
上為減函數(shù),在 上為增函數(shù).
上為增函數(shù).
①當(dāng) ,即
,即 時,
時,
在區(qū)間 上,
上, 在
在 上為減函數(shù),在
上為減函數(shù),在 上為增函數(shù).
上為增函數(shù).
所以 . ………………………10分
. ………………………10分
②當(dāng) ,即
,即 時,
時, 在區(qū)間
在區(qū)間 上為減函數(shù).
上為減函數(shù).
所以 .
.
綜上所述,當(dāng) 時,
時, ;
;
當(dāng) 時,
時,
若函數(shù)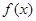 在定義域內(nèi)存在區(qū)間
在定義域內(nèi)存在區(qū)間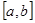 ,滿足
,滿足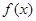 在
在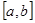 上的值域為
上的值域為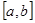 ,則稱這樣的函數(shù)
,則稱這樣的函數(shù)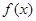 為“優(yōu)美函數(shù)”.
為“優(yōu)美函數(shù)”.
(Ⅰ)判斷函數(shù)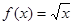 是否為“優(yōu)美函數(shù)”?若是,求出
是否為“優(yōu)美函數(shù)”?若是,求出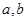 ;若不是,說明理由;
;若不是,說明理由;
(Ⅱ)若函數(shù)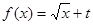 為“優(yōu)美函數(shù)”,求實(shí)數(shù)
為“優(yōu)美函數(shù)”,求實(shí)數(shù)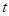 的取值范圍.
的取值范圍.
【解析】第一問中,利用定義,判定由題意得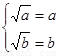 ,由
,由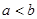 ,所以
,所以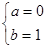
第二問中, 由題意得方程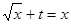 有兩實(shí)根
有兩實(shí)根
設(shè)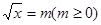 所以關(guān)于m的方程
所以關(guān)于m的方程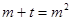 在
在 有兩實(shí)根,
有兩實(shí)根,
即函數(shù)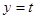 與函數(shù)
與函數(shù)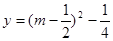 的圖像在
的圖像在 上有兩個不同交點(diǎn),從而得到t的范圍。
上有兩個不同交點(diǎn),從而得到t的范圍。
解(I)由題意得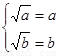 ,由
,由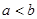 ,所以
,所以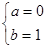 (6分)
(6分)
(II)由題意得方程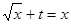 有兩實(shí)根
有兩實(shí)根
設(shè)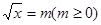 所以關(guān)于m的方程
所以關(guān)于m的方程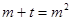 在
在 有兩實(shí)根,
有兩實(shí)根,
即函數(shù)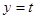 與函數(shù)
與函數(shù)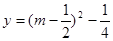 的圖像在
的圖像在 上有兩個不同交點(diǎn)。
上有兩個不同交點(diǎn)。
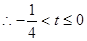
已知函數(shù)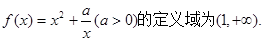
(I)討論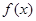 在其定義域上的單調(diào)性;
在其定義域上的單調(diào)性;
(II)當(dāng)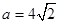 時,若關(guān)于x的方程
時,若關(guān)于x的方程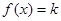 恰有兩個不等實(shí)根,求實(shí)數(shù)k的取值范圍。
恰有兩個不等實(shí)根,求實(shí)數(shù)k的取值范圍。
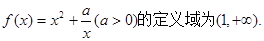
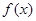 在其定義域上的單調(diào)性;
在其定義域上的單調(diào)性;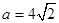 時,若關(guān)于x的方程
時,若關(guān)于x的方程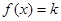 恰有兩個不等實(shí)根,求實(shí)數(shù)k的取值范圍。
恰有兩個不等實(shí)根,求實(shí)數(shù)k的取值范圍。 已知函數(shù)![]()
(I)判斷函數(shù)![]() 上的單調(diào)性,并求出
上的單調(diào)性,并求出![]() 的值;
的值;
(II)求函數(shù)![]() 的單調(diào)區(qū)間及其在定義域上的最小值;
的單調(diào)區(qū)間及其在定義域上的最小值;
(III)是否存在實(shí)數(shù)m,n,滿足![]() ,使得函數(shù)
,使得函數(shù)![]() 的值域也有[m,n]?并說明理由。
的值域也有[m,n]?并說明理由。
一、選擇題:本大題共12個小題,每小題5分,共60分。
1―5 BCBAB 6―10 DCCCD 11―12 DB
二、填空題:本大題共4個小題,每小題4分,共16分。
13.%20高三年級期末測試?yán)砜茢?shù)學(xué)試題.files/image151.gif) 14.1:2 15.①②⑤ 16.⑤
14.1:2 15.①②⑤ 16.⑤